题目内容
【题目】数学活动小组组织一次登山活动,他们从山脚下![]() 点出发沿斜坡
点出发沿斜坡![]() 到达
到达![]() 点,再从
点,再从![]() 点沿斜坡
点沿斜坡![]() 到达山顶
到达山顶![]() 点,路线如图所示.斜坡
点,路线如图所示.斜坡![]() 的长为
的长为![]() 米,斜坡
米,斜坡![]() 的长为
的长为![]() 米,坡度是
米,坡度是![]() ,已知
,已知![]() 点海拔
点海拔![]() 米,
米,![]() 点海拔
点海拔![]() 米.
米.

![]() 问
问![]() 点测得
点测得![]() 点的俯角为________
点的俯角为________![]() ,并求
,并求![]() 点的海拔;
点的海拔;
![]() 求斜坡
求斜坡![]() 的坡度;
的坡度;
![]() 为了方便上下山,若在
为了方便上下山,若在![]() 到
到![]() 之间架设一条钢缆,求钢缆
之间架设一条钢缆,求钢缆![]() 的长度.
的长度.
【答案】(1)45°,![]() 米;(2)坡度为
米;(2)坡度为![]() ;(3)
;(3)![]() 米.
米.
【解析】
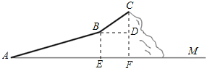
(1)过C作CF⊥AM,F为垂足,过B点作BE⊥AM,BD⊥CF,E、D为垂足,根据斜坡BC的坡度是1:1,可得∠CBD=45°,继而可求得CD的长度,求出B点的高度;
(2)根据(1)中求得B点的高度,AB=200![]() 米,利用勾股定理求出AE的长度,易求得AB的坡度;
米,利用勾股定理求出AE的长度,易求得AB的坡度;
(3)根据CF⊥AM,BE⊥AM,BD⊥CF,得出四边形EFDB是矩形,继而可求得AF=800米,CF=600米,利用勾股定理即可求得AC的长度.
![]() 如图,过
如图,过![]() 作
作![]() ,
,![]() 为垂足,过
为垂足,过![]() 点作
点作![]() ,
,![]() ,
,![]() 、
、![]() 为垂足,
为垂足,
∵斜坡![]() 的坡度是
的坡度是![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴在![]() 点测得
点测得![]() 点的俯角为
点的俯角为![]() ,
,
∴![]() ,又
,又![]() 米,
米,
∴![]() (米),
(米),
∵![]() 点海拔
点海拔![]() 米,
米,![]() 点海拔
点海拔![]() 米,
米,
∴![]() (米)
(米)
∴![]() 点的铅直高度为
点的铅直高度为![]() (米),
(米),
即斜坡![]() 点处的高度为
点处的高度为![]() 米;
米;
![]() ∵
∵![]() 米,
米,
∴![]() 米,
米,![]() (米),
(米),
∴![]() 的坡度
的坡度![]() ,
,
故斜坡![]() 的坡度为
的坡度为![]() .
.
![]() ∵
∵![]() ,
,![]() ,
,![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴![]() 米,
米,![]() 米,
米,
∴![]() 米,
米,![]() 米,
米,
∴![]() 米.
米.
即钢缆![]() 的长度为
的长度为![]() 米.
米.

练习册系列答案
相关题目





