题目内容
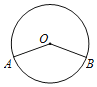
【题目】如图，A，B是⊙O上的两点，C是⊙O上不与A，B重合的任意一点．如果∠AOB＝140°，那么∠ACB的度数为___．
【答案】70°或110°．
【解析】
分点C在优弧上和劣弧上两种情况，根据圆周角定理及圆内接四边形的性质求出∠ACB的度数即可.
如图1，当点C在优弧ACB上时，
∵∠ACB和∠AOB分别是
所对的圆周角和圆心角，
∴∠ACB＝
∠AOB＝70°．
如图2，当点C在劣弧AB上时，在优弧AB上取一点D，连接AD、BD，
∵∠ADB和∠AOB分别是所对的圆周角和圆心角，
∴∠ADB＝∠AOB＝70°，
∵四边形ACBD是⊙O的内接四边形，
∴∠ADB+∠ACB＝180°，
∴∠ACB＝110°．
综上所述：∠ACB的度数为70°或110°．
故答案为70°或110°．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
