Question

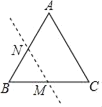
【题目】如图，在等边△ABC中，AB＝4cm，点M为边BC的中点，点N为边AB上的任意一点（不与点A，B重合）．若点B关于直线MN的对称点B'恰好落在等边△ABC的边上，则BN的长为_____cm．

Answer 1

【答案】1或2．

【解析】

如图1，当点B关于直线MN的对称点B'恰好落在等边三角形ABC的边AB上时，于是得到MN⊥AB，BN＝BN′，根据等边三角形的性质得到＝AC＝BC，∠ABC＝60°，根据线段中点的定义得到BN＝BM＝1，如图2，当点B关于直线MN的对称点B'恰好落在等边三角形ABC的边A，C上时，则MN⊥BB′，四边形BMB′N是菱形，根据线段中点的定义即可得到结论．

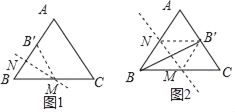
解：如图1，当点B关于直线MN的对称点B'恰好落在等边三角形ABC的边AB上时，

则MN⊥AB，BN＝BN′，

∵△ABC是等边三角形，

∴AB＝AC＝BC，∠ABC＝60°，

∵点M为边BC的中点，

∴BM＝BC＝AB＝2，

∴BN＝BM＝1，

如图2，当点B关于直线MN的对称点B'恰好落在等边三角形ABC的边A，C上时，

则MN⊥BB′，四边形BMB′N是菱形，

∵∠ABC＝60°，点M为边BC的中点，

∴BN＝BM＝BC＝AB＝2，

故答案为：1或2．