题目内容
【题目】已知：如图，
和
均为等腰直角三角形，
，连结
，
，且
、
、
三点在一直线上，
，
．
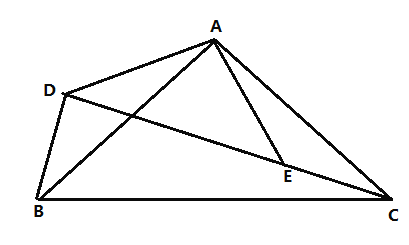
（1）求证：
；
（2）求线段
的长．
【答案】（1）详见解析；（2）
【解析】
（1）根据等式的基本性质可得∠DAB=∠EAC，然后根据等腰直角三角形的性质可得DA=EA，BA=CA，再利用SAS即可证出结论；
（2）根据等腰直角三角形的性质和勾股定理即可求出DE，从而求出EC和DC，再根据全等三角形的性质即可求出DB，∠ADB=∠AEC，从而求出∠BDC=90°，最后根据勾股定理即可求出结论．
证明：（1）∵
∴∠DAE－∠BAE=∠BAC－∠BAE
∴∠DAB=∠EAC
∵
和
均为等腰直角三角形
∴DA=EA，BA=CA
在△ADB和△AEC中
∴△ADB≌△AEC
（2）∵
是等腰直角三角形，
∴DE=
，
∵
∴EC=
，
∴DC=DE＋EC=3
∵△ADB≌△AEC
∴DB=EC=3，∠ADB=∠AEC
∵∠ADB=∠ADE＋∠BDC，∠AEC=∠ADE＋∠DAE=∠ADE＋90°
∴∠BDC=90°
在Rt△BDC中，
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
