题目内容
【题目】如图,一次函数![]() 的图象与
的图象与![]() 和
和![]() 分别交于点
分别交于点![]() 和点
和点![]() ,与正比例函数
,与正比例函数![]() 图象交于点
图象交于点![]() .
.
(1)求![]() 和
和![]() 的值
的值
(2)求![]() 的面积
的面积
(3)在直线![]() 上是否存在异与点
上是否存在异与点![]() 的另一点
的另一点![]() ,使得
,使得![]() 与
与![]() 的面积相等?若存在,请求出
的面积相等?若存在,请求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
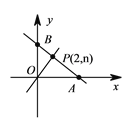
【答案】(1)![]() ,
,![]() ;(2)5;(3)存在,
;(2)5;(3)存在,![]() .
.
【解析】
试题(1)把点P的坐标代入正比例函数![]() 中,可求出n的值,即可知P的坐标,再把P的坐标代入一次函数y=-x+m中,可求出m的值;(2)
中,可求出n的值,即可知P的坐标,再把P的坐标代入一次函数y=-x+m中,可求出m的值;(2)![]() 的面积等于
的面积等于![]() ;(3)根据面积相等,求出点C到OB的距离为2,可得出C的横坐标的值,再根据点C在一次函数的图象上,即可求出C的纵坐标;
;(3)根据面积相等,求出点C到OB的距离为2,可得出C的横坐标的值,再根据点C在一次函数的图象上,即可求出C的纵坐标;
试题解析:
(1)将![]() 代入
代入![]() 中,得
中,得![]()
![]()
将![]() 代入
代入![]() 中,得
中,得![]()
![]() ,
,![]()
(2)因为点B是一次函数y=-x+5与y轴的交点,
所以点B的坐标是(0,5)
![]()
(3)存在,![]()
因为![]() 与
与![]() 的面积相等,且
的面积相等,且![]() ,
,
所以![]() ,
,
又因为OB=5,
所以点C到OB的距离为2,
所以点C的横坐标为2或-2,
又因为点P的横坐标为2,
所以点C的横坐标为-2,
又因为点C在一次函数y=1.5x上,
所以点C的纵坐标为-3,
所以点C的坐标为(-2,-3).

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案
相关题目
【题目】足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度![]() (单位:
(单位:![]() )与足球被踢出后经过的时间
)与足球被踢出后经过的时间![]() (单位:
(单位:![]() )之间的关系如下表:
)之间的关系如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论:①足球距离地面的最大高度为![]() ;②足球飞行路线的对称轴是直线
;②足球飞行路线的对称轴是直线![]() ;③足球被踢出
;③足球被踢出![]() 时落地;④足球被踢出
时落地;④足球被踢出![]() 时,距离地面的高度是
时,距离地面的高度是![]() .
.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4