题目内容
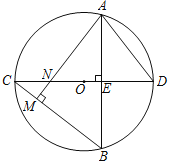
 【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,且BF是⊙O的切线,BF交AC的延长线于F.
【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,且BF是⊙O的切线,BF交AC的延长线于F.
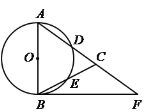
(1)求证:∠CBF=![]() ∠CAB. (2)若AB=5,sin∠CBF=
∠CAB. (2)若AB=5,sin∠CBF=![]() ,求BC和BF的长.
,求BC和BF的长.
【答案】(1)证明略;(2)BC=![]() ,BF=
,BF=![]() .
.
【解析】
试题(1)连结AE.有AB是⊙O的直径可得∠AEB=90°再有BF是⊙O的切线可得BF⊥AB,利用同角的余角相等即可证明;
(2)在Rt△ABE中有三角函数可以求出BE,又有等腰三角形的三线合一可得BC=2BE,
过点C作CG⊥AB于点G.可求出AE,再在Rt△ABE中,求出sin∠2,cos∠2.然后再在Rt△CGB中求出CG,最后证出△AGC∽△ABF有相似的性质求出BF即可.
试题解析:
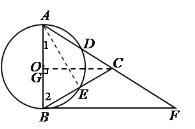
(1)证明:连结AE.∵AB是⊙O的直径, ∴∠AEB=90°,∴∠1+∠2=90°.
∵BF是⊙O的切线,∴BF⊥AB, ∴∠CBF +∠2=90°.∴∠CBF =∠1.
∵AB=AC,∠AEB=90°, ∴∠1=![]() ∠CAB.
∠CAB.
∴∠CBF=![]() ∠CAB.
∠CAB.

(2)解:过点C作CG⊥AB于点G.∵sin∠CBF=![]() ,∠1=∠CBF, ∴sin∠1=
,∠1=∠CBF, ∴sin∠1=![]() .
.
∵∠AEB=90°,AB=5. ∴BE=AB·sin∠1=![]() .
.
∵AB=AC,∠AEB=90°, ∴BC=2BE=![]() .
.
在Rt△ABE中,由勾股定理得![]() .
.
∴sin∠2=![]() ,cos∠2=
,cos∠2=![]() .
.
在Rt△CBG中,可求得GC=4,GB=2. ∴AG=3.
∵GC∥BF, ∴△AGC∽△ABF. ∴![]() ,
,
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目