题目内容
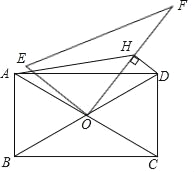
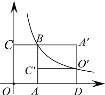
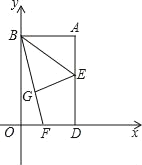
【题目】如图,以矩形ABOD的两边OD、OB为坐标轴建立直角坐标系,若E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交OD于F点.若OF=I,FD=2,则G点的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
连结EF,作GH⊥x轴于H,根据矩形的性质得AB=OD=OF+FD=3,再根据折叠的性质得BA=BG=3,EA=EG,∠BGE=∠A=90°,而AE=DE,则GE=DE,于是可根据“HL”证明Rt△DEF≌Rt△GEF,得到FD=FG=2,则BF=BG+GF=5.在Rt△OBF中,利用勾股定理计算出OB,然后根据△FGH∽△FBO,利用相似比计算出GH和FH,根据OH=OF﹣HF,即可得到G点的坐标.
连结EF,作GH⊥x轴于H,如图,
∵四边形ABOD为矩形,
∴AB=OD=OF+FD=1+2=3.
∵△ABE沿BE折叠后得到△GBE,
∴BA=BG=3,EA=EG,∠BGE=∠A=90°.
∵点E为AD的中点,
∴AE=DE,
∴GE=DE.
在Rt△DEF和Rt△GEF中,
∵![]() ,
,
∴Rt△DEF≌Rt△GEF(HL),
∴FD=FG=2,
∴BF=BG+GF=3+2=5.
在Rt△OBF中,OF=1,BF=5,
∴OB![]() .
.
∵GH∥OB,
∴△FGH∽△FBO,
∴![]() ,
,
即![]() ,
,
∴GH![]() ,FH
,FH![]() ,
,
∴OH=OF﹣HF=1![]() ,
,
∴G点坐标为(![]() ).
).
故选B.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案【题目】某甜品店用 A,B 两种原料制作成甲、乙两款甜品进行销售,制作每份甜品的原料所需用量如下表所示.该店制作甲款甜品 x 份,乙款甜品 y 份,共用去A 原料 2000 克.
原料 款式 | A 原料(克) | B 原料(克) |
甲款甜品 | 30 | 15 |
乙款甜品 | 10 | 20 |
(1)求 y 关于 x 的函数表达式.
(2)已知每份甲甜品的利润为 a 元(a 正整数), 每份乙甜品的利润为 2 元. 假设两款甜品均能全部卖出.
①当 a=3 时,若获得总利润不少于 220 元,则至少要用去 B 原料多少克?
②现有 B 原料 3100 克,要使获利为 450 元且尽量不浪费原材料,甲甜品的每份利润应定为多元?
【题目】小王是“新星厂”的一名工人,请你阅读下列信息:
信息一:工人工作时间:每天上午8:00—12:00,下午14:00—18:00,每月工作25天;
信息二:小王生产甲、乙两种产品的件数与所用时间的关系见下表:
生产甲种产品数(件) | 生产乙种产品数(件) | 所用时间(分钟) |
10 | 10 | 350 |
30 | 20 | 850 |
信息三:按件计酬,每生产一件甲种产品得1.50元,每生产一件乙种产品得2.80元;
信息四:该厂工人每月收入由底薪和计酬工资两部分构成,小王每月的底薪为1900元.请根据以上信息,解答下列问题:
(1)小王每生产一件甲种产品和一件乙种产品分别需要多少分钟;
(2)2018年1月工厂要求小王生产甲种产品的件数不少于60件,则小王该月收入最多是多少元?此时小王生产的甲、乙两种产品分别是多少件?