题目内容
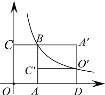
【题目】如图,矩形 OABC 的顶点 O 在坐标原点,顶点 A,C 分别在 x,y 轴的正半轴上,顶点 B 在反比例函数 y ![]() (k 为常数,k>0,x>0)的图象上,将矩形 OABC 绕点 B 逆时针方向旋转 90°得到矩形 BCOA ,点 O 的对应点O 恰好落在此反比例函数图象上.延长 AO ,交 x轴于点 D,若四边形CADO 的面积为 2,则 k 的值为( )
(k 为常数,k>0,x>0)的图象上,将矩形 OABC 绕点 B 逆时针方向旋转 90°得到矩形 BCOA ,点 O 的对应点O 恰好落在此反比例函数图象上.延长 AO ,交 x轴于点 D,若四边形CADO 的面积为 2,则 k 的值为( )
A. ![]() +1B.
+1B. ![]() -1C. 2
-1C. 2 ![]() +2D. 2
+2D. 2 ![]() -2
-2
【答案】A
【解析】
设B(m,n),则OA=m,OC=n,根据旋转的性质得到O'C'=n,A'O'=m,于是得到O'(m+n,n﹣m),于是得到方程(m+n)(n﹣m)=mn,由四边形CADO 的面积为 2,得到(n-m)n=2,解方程即可得到m、n的值,由k=mn即可得到结论.
设B(m,n),则OA=m,OC=n.
∵矩形 OABC 绕点 B 逆时针方向旋转 90°得到矩形 BCOA,∴O'C'=n,A'O'=m,∴A'(m+n,n)∴O'(m+n,n﹣m).
∵四边形CADO 的面积为 2,∴(n-m)n=2,∴n2=2+mn.
∵B,O'在此反比例函数图象上,∴(m+n)(n﹣m)=mn,∴m2+mn﹣n2=0,∴m2+mn-2-mn=0,∴m=±![]() (负值舍去),∴m=
(负值舍去),∴m=![]() ,∴
,∴![]() ,解得:n=
,解得:n=![]() (负值舍去),∴n=
(负值舍去),∴n=![]() ,∴k=mn=
,∴k=mn=![]() =
=![]() .
.
故选A.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目