Question

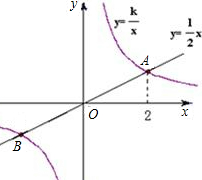
已知正比例函数y=kx与反比例函数y=

3

x

的图象都过A（m，1）点．
求：（1）正比例函数的解析式；
（2）正比例函数与反比例函数的另一个交点的坐标．

Answer 1

分析：（1）将A（m，1）点代入反比例函数y=

3

x

，求得m的值．再将A点坐标代入正比例函数y=kx，求得正比例函数的解析式；
（2）解正比例函数与反比例函数联立的方程组就可以求出正比例函数与反比例函数的另一个交点的坐标．

解答：解：
（1）把x=m，y=1代入y=

3

x

3

m

=1，m=3
∴A（3，1）
把x=3，y=1代入y=kx得
3k=1，k=

1

3

∴y=

1

3

x
（2）解方程组

y= 1 3 x y= 3 x

解得

x1=3 y1=1

，

x2=-3 y2=-1

故另一交点的坐标为（-3，-1）．

点评：本题综合考查待定系数法求函数解析式与方程组的相关知识点．先由点的坐标求函数解析式，然后解由解析式组成的方程组求出交点的坐标．