题目内容
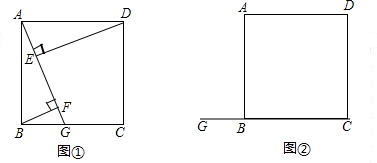
如图，E是正方形ABCD的边CD延长线上的任意一点，CF⊥AE于点F，交AD于点H．求∠DHE的度数．
∵四边形ABCD是正方形，
∴CD=AD，∠CDH=∠ADE=90°，
∵CF⊥AE，
∴∠AFH=90°，
∴∠HCD+∠CHD=∠AHF+∠DAE=90°
∵∠AHF=∠CHD，
∴∠DCH=∠DAE，
在△CDH和△ADE中
∴△CDH≌△ADE，
∴DH=DE，
∵∠HDE=90°，
∴∠DHE=∠DEH=45°．
∴CD=AD，∠CDH=∠ADE=90°，
∵CF⊥AE，
∴∠AFH=90°，
∴∠HCD+∠CHD=∠AHF+∠DAE=90°
∵∠AHF=∠CHD，
∴∠DCH=∠DAE，
在△CDH和△ADE中
|
∴△CDH≌△ADE，
∴DH=DE，
∵∠HDE=90°，
∴∠DHE=∠DEH=45°．
练习册系列答案
相关题目
，连接DF，交BE的延长线于点G，连接OG．
