题目内容
已知:如图,在平面直角坐标系 中,抛物线
中,抛物线 过点A(6,0)和点B(3,
过点A(6,0)和点B(3,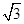 ).
).
(1)求抛物线 的解析式;
的解析式;
(2)将抛物线 沿x轴翻折得抛物线
沿x轴翻折得抛物线 ,求抛物线
,求抛物线 的解析式;
的解析式;
(3)在(2)的条件下,抛物线 上是否存在点M,使
上是否存在点M,使 与
与 相似?如果存在,求出点M的坐标;如果不存在,说明理由.
相似?如果存在,求出点M的坐标;如果不存在,说明理由.
(1) 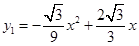 ;(2)
;(2) ;(3)
;(3) ,
,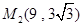 ,
, .
.
解析试题分析:(1)把A、B两点坐标代入y1=ax2+bx,求得a、b的值,从而确定y1的解析式;
(2)将抛物线 沿x轴翻折后,仍过点O(0,0),A(6,0),还过点B关于x轴的对称点
沿x轴翻折后,仍过点O(0,0),A(6,0),还过点B关于x轴的对称点 .从而可求y2的解析式;
.从而可求y2的解析式;
(3)过点B作BC⊥x轴于点C,易证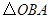 是顶角为120º的等腰三角形.分两种情况讨论:①当点M在x轴下方时,
是顶角为120º的等腰三角形.分两种情况讨论:①当点M在x轴下方时, 就是
就是 ,此时点M的坐标为
,此时点M的坐标为 .②当点M在x轴上方时,此时点M的坐标为(9,
.②当点M在x轴上方时,此时点M的坐标为(9, )、
)、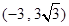 .
.
试题解析:(1)依题意,得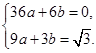 解得
解得
∴抛物线 的解析式为
的解析式为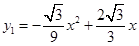
(2)将抛物线 沿x轴翻折后,仍过点O(0,0),A(6,0),还过点B关于x轴的对称点
沿x轴翻折后,仍过点O(0,0),A(6,0),还过点B关于x轴的对称点 .
.
设抛物线 的解析式为
的解析式为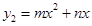 ,
,
∴ 解得
解得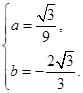
∴抛物线 的解析式为
的解析式为 .
.
(3)过点B作BC⊥x轴于点C,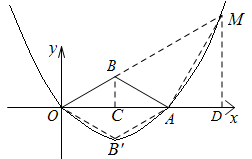
则有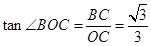 .
.
∴ ,
,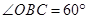 .
.
∵OC=3,OA=6,
∴AC=3.
∴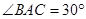 ,
,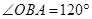 .
.
∴OB=AB.
即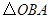 是顶角为120º的等腰三角形.
是顶角为120º的等腰三角形.
分两种情况:
①当点M在x轴下方时, 就是
就是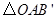 ,此时点M的坐标为
,此时点M的坐标为 .
.
②当点M在x轴上方时,假设
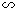
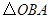 ,则有AM=OA=6,
,则有AM=OA=6,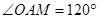 .
.
过点M作MD⊥x轴于点D,则 .
.
∴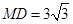 ,
,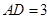 . ∴OD=9.
. ∴OD=9.
而(9, )满足关系式
)满足关系式 ,
,
即点M在抛物线 上.
上.
根据对称性可知,点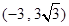 也满足条件.
也满足条件.
综上所述,点M的坐标为 ,
,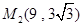 ,
, .
.
考点:二次函数综合题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
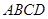 中,
中,  , 高
, 高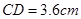 (如图1). 动点
(如图1). 动点 同时从点
同时从点 出发, 点
出发, 点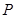 沿
沿 运动到点
运动到点 停止, 点
停止, 点 沿
沿 运动到点
运动到点 时,点
时,点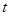 (s)时,
(s)时,  的面积为
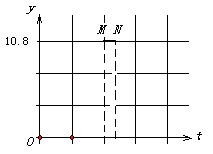
的面积为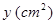 (如图2). 分别以
(如图2). 分别以 为横、纵坐标建立直角坐标系, 已知点
为横、纵坐标建立直角坐标系, 已知点 边上从
边上从 运动时,
运动时,  与
与 .
.

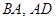 的长度;
的长度; 边上和
边上和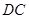 边上运动时,
边上运动时,  经过点A和点C,动点P在x轴上以每秒1个长度单位的速度由抛物线与x轴的另一个交点B向点A运动,点Q由点C沿线段CA向点A运动且速度是点P运动速度的2倍.
经过点A和点C,动点P在x轴上以每秒1个长度单位的速度由抛物线与x轴的另一个交点B向点A运动,点Q由点C沿线段CA向点A运动且速度是点P运动速度的2倍.
 与x轴交于A、C两点,与y轴交于B点.
与x轴交于A、C两点,与y轴交于B点.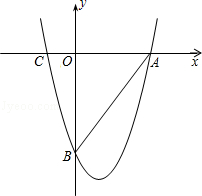
 ,
, ).
).

 .
.
 的解集.
的解集. x2+10,并且BD=
x2+10,并且BD= CD.
CD.
