题目内容
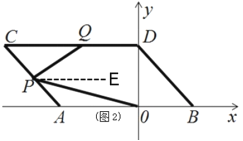
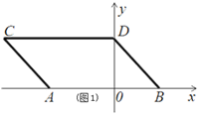
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0).且a,b满足![]() +(a-2b+7)2=0.现同时将点A,B分别向左平移2个单位,再向上平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD.
+(a-2b+7)2=0.现同时将点A,B分别向左平移2个单位,再向上平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD.
(1)请直接写出A,B两点的坐标.
(2)如图,点P是线段AC上的一个动点,点Q是线段CD的中点,连接PQ,PO,当点P在线段AC上移动 时(不与A,C重合),请找出∠PQD,∠OPQ,∠POB的数量关系,并证明你的结论.
(3)在坐标轴上是否存在点M,使三角形MAD的面积与三角形ACD的面积相等?若存在,直接写出点M的坐标;若不存在,试说明理由.

【答案】(1) A(-3,0) B(2,0);
【解析】
(1)根据平方与绝对值的非负性即可求解;(2)过点P作PE∥AB,由平移的性质可得AB∥CD,利用平行线的性质即可求解;(3)先求出△ACD的面积,再根据M在x轴上与y轴上分别求解.
解:(1)依题意得![]() =0,a-2b+7=0,解得a=-3,b=2,
=0,a-2b+7=0,解得a=-3,b=2,
∴A(-3,0) B(2,0)
∵将点A,B分别向左平移2个单位,再向上平移2个单位,分别得到点A,B的对应点C,D,
∴C(-5,2),D(0,2)
(2)∠PQD+∠OPQ+∠POB=360°
证明:过点P作PE∥AB,由平移的性质可得AB∥CD,
∴AB∥PE∥CD,
∴∠PQD+∠EPQ =180°,∠OPE +∠POB=180°,
∴∠PQD+∠EPQ+∠OPE +∠POB=360°,
即∠PQD+∠OPQ+∠POB=360°
(3) 先求出△ACD的面积为![]() =5
=5
①M在x轴上
再根据△MAD的高与△ACD相等即AM=CD=5,故坐标为(-8,0),(2,0),
②M在y轴上,根据△MAD的高为AO=3,得出MD=![]()
由D(0,2)
得出M(0,![]() ),(0,
),(0,![]() ).
).
故存在符合条件的M点坐标为(-8,0),(2,0),(0,![]() ),(0,
),(0,![]() ).
).