题目内容
【题目】点O在△ABC的内部,点D,E,F,G分别是AB,OB,OC,AC的中点.
(1)如图1,求证:四边形DEFG是平行四边形;
(2)如图2,射线AO交BC边于点H,连接DH,GH,若AB=AC,DE⊥EF,在不添加任何辅助线的情况下,请直接写出图2中所有的等腰三角形(不包含以∠BAC为内角的三角形).
【答案】(1)见解析;(2)△OBC,△OEF,△HGC,△HGA,△BDH,△DHA.
【解析】
(1)只要证明DG∥EF,DG=EF即可.
(2)首先证明AH垂直平分BC,得到△OBC,△OEF是等腰三角形,再根据直角三角形斜边中线性质得到△HGC,△HGA,△BDH,△DHA是等腰三角形.
(1)证明:如图1中,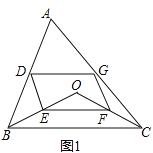
∵AD=DB,AG=GC,
∴DG∥BC,DG=![]() BC,
BC,
∵OE=EB,OF=FC,
∴EF∥BC,EF=![]() BC,
BC,
∴DG∥EF,EF=DG,
∴四边形DEFG是平行四边形.
(2)如图2中,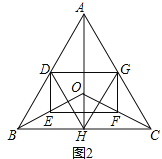
∵BD=DA,BE=EO,
∴DE∥AO,
∵EF∥BC,DE⊥EF,
∴DE⊥BC,
∴AH⊥BC,
∵AB=AC,
∴BH=HC,
∴OB=OC,OE=OF,
∴△OBC,△OEF是等腰三角形,
∵DH是Rt△ABH斜边中线,
∴DH=BD=AD,
∴△BDH,△DHA是等腰三角形,同理△HGC,△HGA都是等腰三角形.
综上所述等腰三角形有△OBC,△OEF,△HGC,△HGA,△BDH,△DHA.

【题目】中央电视台的《朗读者》节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本数量少的有![]() 本,最多的有
本,最多的有![]() 本,并根据调查结果绘制了不完整的图表,如下所示:
本,并根据调查结果绘制了不完整的图表,如下所示:
本数(本) | 频数(人数) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|

(![]() )统计图表中的
)统计图表中的![]() __________,
__________,![]() __________,
__________,![]() __________.
__________.
(![]() )请将频数分布直方图补充完整.
)请将频数分布直方图补充完整.
(![]() )求所有被调查学生课外阅读的平均本数.
)求所有被调查学生课外阅读的平均本数.
(![]() )若该校八年级共有
)若该校八年级共有![]() 名学生,请你估计该校八年级学生课外阅读
名学生,请你估计该校八年级学生课外阅读![]() 本及以上的人数.
本及以上的人数.