��Ŀ����
����Ŀ������ABC�Ƶ�A����ʱ�뷽����ת�ȶȣ���ʹ���߳���Ϊԭ����n�����á�AB��C�䣬��ͼ����ʾ����BAB��=�ȣ� ![]() =
= ![]() =
= ![]() =n�����ǽ����ֱ任��Ϊ[�ȣ�n]��
=n�����ǽ����ֱ任��Ϊ[�ȣ�n]��
��1����ͼ�٣��ԡ�ABC���任[60�㣬 ![]() ]�õ���AB��C�䣬��S��AB'C��S��ABC=��ֱ��BC��ֱ��B��C�����е����Ϊ�ȣ�
]�õ���AB��C�䣬��S��AB'C��S��ABC=��ֱ��BC��ֱ��B��C�����е����Ϊ�ȣ�
��2����ͼ�ڣ���ABC�У���BAC=30�㣬��ACB=90�㣬�ԡ�ABC���任[�ȣ�n]�õ���AB��C�䣬ʹ��B��C��C����ͬһֱ���ϣ����ı���ABB��C��Ϊ���Σ���Ⱥ�n��ֵ��
��3����ͼ�ۣ���ABC�У�AB=AC����BAC=36�㣬BC=1���ԡ�ABC���任[�ȣ�n]�õ���AB��C�䣬ʹ��B��C��B����ͬһֱ���ϣ����ı���ABB��C��Ϊƽ���ı��Σ���Ⱥ�n��ֵ��
���𰸡�
��1��3��60
��2��
�⣺��ͼ���У�

���ı���ABB��C���Ǿ��Σ�
���BAC��=90�㣮
���=��CAC��=��BAC�䩁��BAC=90�㩁30��=60�㣮
��Rt��ABB���У���ABB��=90�㣬��BAB��=60�㣬
��n= ![]() =2��
=2��
��3��
�⣺��ͼ���У�
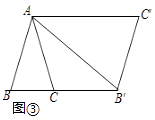
���ı���ABB��C����ƽ���ı��Σ���AC���BB�䣬
�֡ߡ�BAC=36�㣬
���=��CAC��=��ACB=72��
���C��AB��=��ABB��=��BAC=36�㣬
���=��BAB��=72�㣬
�֡ߡ�B=��B��
���ABC�ס�B��BA��
��AB2=CBB��B=CB��BC+CB�䣩��
��CB��=AC=AB=B��C�䣬BC=1��
��AB2=1��1+AB��
��AB= ![]() ��
��
��AB��0��
��n= ![]() =
= ![]() ��
��
���������⣺��1����ͼ���У���ֱ��BC��ֱ��B��C��Ľ���ΪH��AB�佻BH��O��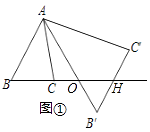
�ߡ�ABC�ס�AB��C�䣬
AB��AB��= ![]() ��
��
��S��ABC��S��AB��C��=3��
�ߡ�B=��B�䣬��AOB=��HOB�䣬
���OHB=��BAO=60�㣬
�ʴ�Ϊ3��60�㣮
��1�����ݱ任[60�㣬 ![]() ]�Ķ��壬���ɽ�����⣮��2����취�����CAC�䣬�Լ�
]�Ķ��壬���ɽ�����⣮��2����취�����CAC�䣬�Լ� ![]() ��ֵ���ɣ���3����취�����BAB�䣬�Լ�
��ֵ���ɣ���3����취�����BAB�䣬�Լ� ![]() ��ֵ����
��ֵ����

 ��Կ���Ծ�ϵ�д�
��Կ���Ծ�ϵ�д�