题目内容
【题目】如图,DE是⊙O的直径,弦AB⊥CD,垂足为C,若AB=6,CE=1,则OC= , CD= . 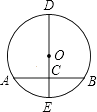
【答案】4;9
【解析】解:连接OA, ∵直径DE⊥AB,且AB=6
∴AC=BC=3,
设圆O的半径OA的长为x,则OE=OD=x
∵CE=1,
∴OC=x﹣1,
在Rt△AOC中,根据勾股定理得:
x2﹣(x﹣1)2=32 , 化简得:x2﹣x2+2x﹣1=9,
即2x=10,
解得:x=5
所以OE=5,则OC=OE﹣CE=5﹣1=4,CD=OD+OC=9.
所以答案是:4;9
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对垂径定理的理解,了解垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( ) 
A.函数有最小值
B.对称轴是直线x= ![]()
C.当x< ![]() ,y随x的增大而减小
,y随x的增大而减小
D.当﹣1<x<2时,y>0
【题目】某种商品的进价为40元/件,以获利不低于25%的价格销售时,商品的销售单价y(元/件)与销售数量x(件)(x是正整数)之间的关系如下表:
x(件) | … | 5 | 10 | 15 | 20 | … |
y(元/件) | … | 75 | 70 | 65 | 60 | … |
(1)由题意知商品的最低销售单价是___元,当销售单价不低于最低销售单价时,y是x的一次函数.求出y与x的函数关系式及x的取值范围;
(2)在(1)的条件下,当销售单价为多少元时,所获销售利润最大,最大利润是多少元?