Question

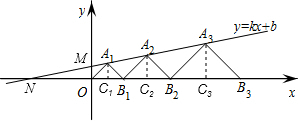
在平面直角坐标系xOy中，点A₁，A₂，A₃，…和B₁，B₂，B₃，…分别在直线y=kx+b和x轴上．△OA₁B₁，△B₁A₂B₂，△B₂A₃B₃，…都是等腰直角三角形，如果A₁（1，1），A₂（

7

2

，

3

2

），那么点A_n的纵坐标是______．

Answer 1

∵A₁（1，1），A₂（

7

2

，

3

2

）在直线y=kx+b上，
∴

k+b=1 7 2 k+b= 3 2

，
解得

k= 1 5 b= 4 5

，
∴直线解析式为y=

1

5

x+

4

5

，
如图，设直线与x轴、y轴的交点坐标分别为N、M，
当x=0时，y=

4

5

，
当y=0时，

1

5

x+

4

5

=0，解得x=-4，
∴点M、N的坐标分别为M（0，

4

5

），N（-4，0），
∴tan∠MNO=

MO

NO

=

4 5

4

=

1

5

，
作A₁C₁⊥x轴于点C₁，A₂C₂⊥x轴于点C₂，A₃C₃⊥x轴于点C₃，
∵A₁（1，1），A₂（

7

2

，

3

2

），
∴OB₂=OB₁+B₁B₂=2×1+2×

3

2

=2+3=5，
tan∠MNO=

A3C3

NC3

=

A3C3

4+5+B2C3

=

1

5

，
∵△B₂A₃B₃是等腰直角三角形，
∴A₃C₃=B₂C₃，
∴A₃C₃=

9

4

=（

3

2

）²，
同理可求，第四个等腰直角三角形A₄C₄=

27

8

=（

3

2

）³，
依此类推，点A_n的纵坐标是（

3

2

）^n-1．
故答案为：（

3

2

）^n-1．