题目内容
已知Rt△ 的两直角边的长都是方程
的两直角边的长都是方程 的根,则Rt△
的根,则Rt△ 的斜边长可能是 .(写出所有可能的值)
的斜边长可能是 .(写出所有可能的值)
 的两直角边的长都是方程
的两直角边的长都是方程 的根,则Rt△
的根,则Rt△ 的斜边长可能是 .(写出所有可能的值)
的斜边长可能是 .(写出所有可能的值)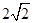 或
或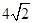 或
或
首先用因式分解法解方程,求出方程的解,再分析所有情况(2 2或4 4或2 4),利用勾股定理即可求出斜边.
解;x2-6x+8=0,
解得:x1=2,x2=4,
∵Rt△ABC的两直角边的长都是方程x2-6x+8=0的根,
∴有以下三种情况:
(1)两直角边是2,2,由勾股定理得:
斜边为: ,
,
(2)两直角边是4,4,
同法可求斜边为:4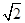 ,
,
(3)两直角边是2,4,
同法可求斜边为:2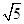 .
.
故答案为:2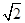 或4
或4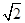 或2
或2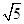 .
.
解;x2-6x+8=0,
解得:x1=2,x2=4,
∵Rt△ABC的两直角边的长都是方程x2-6x+8=0的根,
∴有以下三种情况:
(1)两直角边是2,2,由勾股定理得:
斜边为:
 ,
,(2)两直角边是4,4,
同法可求斜边为:4
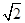 ,
,(3)两直角边是2,4,
同法可求斜边为:2
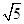 .
.故答案为:2
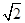 或4
或4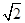 或2
或2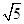 .
.
练习册系列答案
相关题目
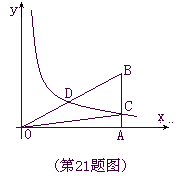
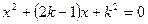 的两根
的两根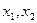 满足
满足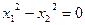 ,双曲线
,双曲线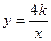 (x>0)经过Rt△OAB斜边OB的中点D,与直角边AB交于C(如图),求
(x>0)经过Rt△OAB斜边OB的中点D,与直角边AB交于C(如图),求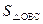 .
.
 .若商店在试销期间每天销售这种商品获得200元的利润,根据题意,下面所列方程正确的是( ).
.若商店在试销期间每天销售这种商品获得200元的利润,根据题意,下面所列方程正确的是( ).



 +n2+2m-6n+10=0的是( )
+n2+2m-6n+10=0的是( )
 的根的判别式
的根的判别式 ____
____