题目内容
如图，O为矩形ABCD的中心，M为BC边上一点，N为DC边上一点，ON⊥OM，若AB=6，AD=4，设OM=x，ON=y，则y与x的函数关系式为________．
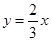
此题主要考查的是相似三角形的判定与性质，解题的关键是合理的在图中作出辅助线，熟练掌握相似三角形的判定定理和性质．
解：
如图，作OF⊥BC于F，OE⊥CD于E，
∵ABCD为矩形，∴∠C=90°.
∵OF⊥BC，OE⊥CD，∴∠EOF=90°
∴∠EON+∠FON=90°.
∵ON⊥OM，
∴∠EON=∠FOM，
∴△OEN∽△OFM，
.
∵O为中心，
∴
.
∴
.
即.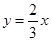
故答案为：.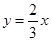
解：
如图，作OF⊥BC于F，OE⊥CD于E，
∵ABCD为矩形，∴∠C=90°.
∵OF⊥BC，OE⊥CD，∴∠EOF=90°
∴∠EON+∠FON=90°.
∵ON⊥OM，
∴∠EON=∠FOM，
∴△OEN∽△OFM，
.∵O为中心，
∴
.∴
.即
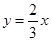.故答案为：
.
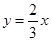练习册系列答案
相关题目
，相似比为1:2，则
与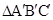
的面积的比为（ ）
的值为 ；
，则△CEF的面积是（ ）
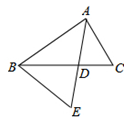
AC，DE=4，那么EF的值是 ．