题目内容
【题目】如图,在△ABC中,D是BC边上的点(不与点B、C重合),连结AD.
问题引入:
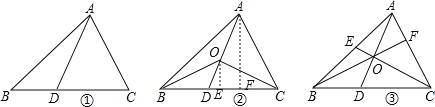
(1)如图①,当点D是BC边上的中点时,S△ABD:S△ABC= ;当点D是BC边上任意一点时,S△ABD:S△ABC= (用图中已有线段表示).
探索研究:
(2)如图②,在△ABC中,O点是线段AD上一点(不与点A、D重合),连结BO、CO,试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比,并说明理由.
拓展应用:
(3)如图③,O是线段AD上一点(不与点A、D重合),连结BO并延长交AC于点F,连结CO并延长交AB于点E,试猜想![]() 的值,并说明理由.
的值,并说明理由.

【答案】(1)1:2,BD:BC;
(2)S△BOC:S△ABC=OD:AD,理由见解析;
(3)![]() =1,理由见解析.
=1,理由见解析.
【解析】
试题分析:(1)根据三角形的面积公式,两三角形等高时,可得两三角形底与面积的关系,可得答案;
(2)根据三角形的面积公式,两三角形等底时,可得两三角形的高与面积的关系,可得答案;
(3)根据三角形的面积公式,两三角形等底时,可得两三角形的高与面积的关系,再根据分式的加减,可得答案.
试题解析:(1)如图①,当点D是BC边上的中点时,S△ABD:S△ABC=1:2;当点D是BC边上任意一点时,S△ABD:S△ABC=BD:BC,
故答案为:1:2,BD:BC;
(2)S△BOC:S△ABC=OD:AD,
如图②作OE⊥BC与E,作AF⊥BC与F,,
∵OE∥AF,
∴△OED∽△AFD,
∴![]() .
.
∵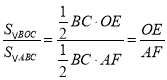 ,
,
∴![]() ;
;
(3)![]() =1,理由如下:
=1,理由如下:
由(2)得![]() ,
,![]() ,
,![]() .
.
∴![]() =
=![]() =
=![]() =1.
=1.
 .
.

练习册系列答案
相关题目