题目内容
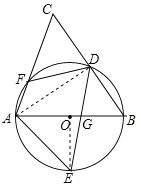
【题目】如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.
(1)证明:∠E=∠C;
(2)若∠E=55°,求∠BDF的度数;
(3)设DE交AB于点G,若DF=4,cosB=![]() ,E是弧AB的中点,求EGED的值.
,E是弧AB的中点,求EGED的值.

【答案】(1)见解析;(2)∠BDF=110°;(3)18
【解析】试题解析:(1)直接利用圆周角定理得出AD⊥BC,劲儿利用线段垂直平分线的性质得出AB=AC,即可得出∠E=∠C;
(2)利用圆内接四边形的性质得出∠AFD=180°﹣∠E,进而得出∠BDF=∠C+∠CFD,即可得出答案;
(3)根据cosB=![]() ,得出AB的长,再求出AE的长,进而得出△AEG∽△DEA,求出答案即可.
,得出AB的长,再求出AE的长,进而得出△AEG∽△DEA,求出答案即可.
试题解析:(1)证明:连接AD,∵AB是⊙O的直径,∴∠ADB=90°,即AD⊥BC,∵CD=BD,∴AD垂直平分BC,∴AB=AC,∴∠B=∠C,又∵∠B=∠E,∴∠E=∠C;
(2)解:∵四边形AEDF是⊙O的内接四边形,∴∠AFD=180°﹣∠E,又∵∠CFD=180°﹣∠AFD,∴∠CFD=∠E=55°,又∵∠E=∠C=55°,∴∠BDF=∠C+∠CFD=110°;
(3)解:连接OE,∵∠CFD=∠E=∠C,∴FD=CD=BD=4,在Rt△ABD中,cosB=![]() ,BD=4,∴AB=6,∵E是
,BD=4,∴AB=6,∵E是![]() 的中点,AB是⊙O的直径,∴∠AOE=90°,∵AO=OE=3,∴AE=
的中点,AB是⊙O的直径,∴∠AOE=90°,∵AO=OE=3,∴AE=![]() ,∵E是
,∵E是![]() 的中点,∴∠ADE=∠EAB,∴△AEG∽△DEA,∴
的中点,∴∠ADE=∠EAB,∴△AEG∽△DEA,∴![]() ,即EGED=
,即EGED=![]() =18.
=18.

练习册系列答案
相关题目