��Ŀ����
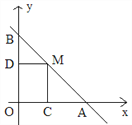
����Ŀ����ͼ��ֱ��y=4��x����������ֱ��ཻ��A��B�㣬��M���߶�AB������һ��(A��B�������)����M�ֱ���MC��OA�ڵ�C��MD��OB�ڵ�D��
(1)����M��AB���˶�ʱ���ı���OCMD���ܳ�Ϊ________��
(2)���ı���OCMDΪ������ʱ����������OCMD����x����������ƶ�����ƽ�Ƶľ���Ϊa (0<a��4)����ƽ�ƹ����У�
�ٵ�ƽ�ƾ���a=1ʱ, ������OCMD����AOB�ص����ֵ����Ϊ________��
�ڵ�ƽ�ƾ���a�Ƕ���ʱ��������OCMD�������ֱ��AB�ֳ�l��3��������?
���𰸡���1��8����2����3.5����a=![]() ��
��![]()
�������������������1�����M�ĺ�����Ϊx�����M��������Ϊ-x+4��0��x��4��x��0��-x+4��0�������ı��ε��ܳ����㷽�����㼴�ɷ��֣�����M��AB���˶�ʱ���ı���OCMD���ܳ��������仯�����ǵ���8��
��2������0��a��2ʱ��S=4-![]() a2=-
a2=-![]() a2+4,����a=1������ص����ֵ������
a2+4,����a=1������ص����ֵ������
�����ı���ΪOCMDΪ������ʱ������������εı߳����Ӷ�����������ε����������������α�ֱ�߷ֳɵĽ�С�IJ��ֵ����Ϊ1��Ȼ����֤������С�IJ�����Ϊ����ֱ�������Σ��Ӷ�����øõ���ֱ�������ε�ֱ�DZߵij��ȣ����ǿ����ƽ�Ƶľ��룮
�����������1����1����OC=x����CM=4-x��
��MC��OA��MD��OB��OD��OC��
���ı���OCMDΪ���Σ�
���ı���OCMD���ܳ�=OD+OC+CM+DM=2��CO+CM��=2��x+4-x��=2��4=8��
��2������ͼ�� 2 ������0��a��2ʱ��S=S������O��CMD-S��MEF=4-![]() a2=-
a2=-![]() a2+4��
a2+4��
�ڡ����ı���ΪOCMDΪ������ʱ��OC=CM����x=4-x����ã�x=2��
��S������OCMD������=4��
��������OCMD�������ֱ��AB�ֳ�1��3�������֣�
�������ֵ�����ֱ�Ϊ1��3��
��0��a��2ʱ����ͼ1��ʾ��

��ֱ��AB�Ľ���ʽΪy=4-x��
���BAO=45����
���MM��EΪ����ֱ�������Σ�
��MM��=M��E��
��![]() MM��2=1��
MM��2=1��
��MM��=![]() ����a=
����a=![]()
��2��a��4ʱ����ͼ2��ʾ��
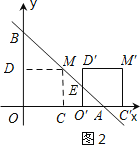
�ߡ�BAO=45����
���EO��AΪ����ֱ�������Σ�
��EO��=O��A��
��![]() O��A2=1����ã�O��A=
O��A2=1����ã�O��A=![]() ��
��
����y=0����y=4-x�ã�4-x=0����ã�x=4��
��OA=4��
��OO��=4-![]() ����a=4-
����a=4-![]() ��
��
������������ƽ�Ƶľ���Ϊa=![]() ��a=4
��a=4![]() ʱ��������OCMD�������ֱ��AB�ֳ�1��3�������֣�
ʱ��������OCMD�������ֱ��AB�ֳ�1��3�������֣�