��Ŀ����
����Ŀ�������꼶����������ʵ����ijɼ������������ֳ�5��С�飨x��ʾ�ɼ�����λ���ף���A�飺5.25��x��6.25��B�飺6.25��x��7.25��C�飺7.25��x��8.25��D�飺8.25��x��9.25��E�飺9.25��x��10.25�������Ƴ�����ͳ��ͼ��Ƶ���ֲ�ֱ��ͼ�������������涨x��6.25Ϊ�ϸ�x��9.25Ϊ���㣮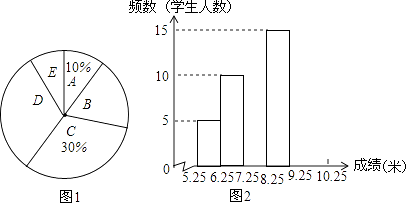
��1���ⲿ�������ж����ˣ����гɼ��ϸ���ж����ˣ�
��2���ⲿ�������ɼ�����λ��������һ�飿����ͳ��ͼ��D���Ӧ��Բ�Ľ��Ƕ��ٶȣ�
��3��Ҫ�ӳɼ������ѧ���У����ѡ��2�˽��ܾ��飬��֪�ס�����λͬѧ�ijɼ���Ϊ���㣬������������1�˱�ѡ�еĸ��ʣ�
���𰸡�
��1���⣺��A��ռ10%����5�ˣ�
���ⲿ���������У�5��10%=50���ˣ���
��ֻ��A�����˳ɼ����ϸ�
��ϸ�����Ϊ��50��5=45���ˣ���
��2���⣺��C��ռ30%������������50��30%=15���ˣ���B����10�ˣ�D����15�ˣ�
����50�������ijɼ��ɵ͵��߷�������A����5�ˣ�B����10�ˣ�C����15�ˣ�D����15�ˣ�E����5�ˣ�
��ɼ�����λ������C�飻
��D����15�ˣ�ռ15��50=30%��
���Ӧ��Բ�Ľ�Ϊ��360���30%=108�㣻
��3���⣺�ɼ������������E�飬���ס���������������������������Ϊa��b��c��
����״ͼ�ã�
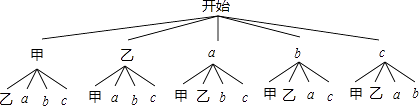
�߹���20�ֵȿ��ܵĽ��������������1�˱�ѡ�е���14�������
������������1�˱�ѡ�еĸ���Ϊ�� ![]() =
= ![]() ��
��
����������1������ͳ��ͼ�У�A��ռ10%����5�ˣ��������������ֻ��A�����˳ɼ����ϸõ��ϸ���������2����C��ռ30%���õ�C����������B����10�ˣ�D����15�ˣ��õ���50�������ijɼ��ɵ͵��߷�������A����5�ˣ�B����10�ˣ�C����15�ˣ�D����15�ˣ�E����5�ˣ��ɼ�����λ������C�飻��D��������������Ӧ��Բ�Ľǣ���3�����ݻ���״ͼ���õ�����20�ֵȿ��ܵĽ��������������1�˱�ѡ�е���14��������õ�����������1�˱�ѡ�еĸ���.

 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д� �߽�������ϵ�д�
�߽�������ϵ�д�