题目内容
△ABC和△A′B′C′中,AB=A′B′,AC=A′C′,∠C=60°AD,A′D′分别为BC,B′C′边上的高,且AD=A′D′,则∠C′的度数为
- A.60°
- B.120°
- C.60°或30°
- D.60°或120°
D
分析:先根据题意画出图形,再利用全等三角形的性质解答,画图时要注意∠C为锐角和钝角两种情况讨论.
解答:当∠C′为锐角时,如图1所示,
∵AC=A′C′,AD=A′D′,AD⊥BC,A′D′⊥B′C′,
∴Rt△ADC≌Rt△A′D′C′,
∴∠C=∠C′=60°;
当∠C为钝角时,如图3所示,
∵AC=A′C′,AD=A′D′,AD⊥BC,A′D′⊥B′C′,
∴Rt△ACD≌Rt△A′C′D′,
∴∠C=∠A′C′D′,
∵∠C=60°,
∴∠A′C′D′=60°,
∴∠A′C′B′=120°,即∠C′=120′.
∴∠C′=60°或120°.
故选D.
点评:本题考查的是全等三角形的判定定理,在解答此题时要注意分∠C为锐角和钝角两种情况讨论,不要漏解.
分析:先根据题意画出图形,再利用全等三角形的性质解答,画图时要注意∠C为锐角和钝角两种情况讨论.
解答:当∠C′为锐角时,如图1所示,
∵AC=A′C′,AD=A′D′,AD⊥BC,A′D′⊥B′C′,
∴Rt△ADC≌Rt△A′D′C′,

∴∠C=∠C′=60°;
当∠C为钝角时,如图3所示,
∵AC=A′C′,AD=A′D′,AD⊥BC,A′D′⊥B′C′,
∴Rt△ACD≌Rt△A′C′D′,
∴∠C=∠A′C′D′,
∵∠C=60°,
∴∠A′C′D′=60°,
∴∠A′C′B′=120°,即∠C′=120′.
∴∠C′=60°或120°.
故选D.
点评:本题考查的是全等三角形的判定定理,在解答此题时要注意分∠C为锐角和钝角两种情况讨论,不要漏解.

练习册系列答案
相关题目
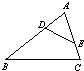 12、如图,要使△ABC和△ADE相似,只需增加的一个条件是
12、如图,要使△ABC和△ADE相似,只需增加的一个条件是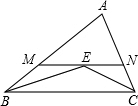 如图,在△ABC中,∠ABC和∠ACB的平分线交于E点,过点E 作MN∥BC交于点M,交AC于N点,若BM+CN=8,则线段MN的长为
如图,在△ABC中,∠ABC和∠ACB的平分线交于E点,过点E 作MN∥BC交于点M,交AC于N点,若BM+CN=8,则线段MN的长为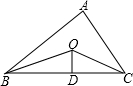 如图,已知△ABC的周长是22,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,△ABC的面积是
如图,已知△ABC的周长是22,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,△ABC的面积是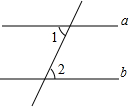 根据题意,把下列推理所依据的命题写出来,并指出是公理还是定理.
根据题意,把下列推理所依据的命题写出来,并指出是公理还是定理.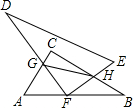 如图,Rt△ABC和Rt△DEF中,∠ACB=∠DFE=90°,F为AB的中点,DF与AC交于点G,EF与BC交于点H,则AG、BH、GH满足的等量关系为
如图,Rt△ABC和Rt△DEF中,∠ACB=∠DFE=90°,F为AB的中点,DF与AC交于点G,EF与BC交于点H,则AG、BH、GH满足的等量关系为