题目内容
以原点O（0，0），A（1.2）为顶点的△AOB是等腰三角形，且点B在坐标轴上，满足条件的点B有 个，其中横纵坐标均为整数的坐标为 ．
考点：等腰三角形的判定,坐标与图形性质
专题：分类讨论
分析：分OA是底边和腰两种情况进行讨论即可确定点B的位置．
解答：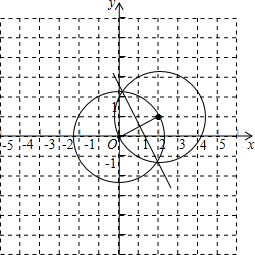
解：当OA是底边时，B在线段OA的中垂线上，与坐标轴有2个交点，则满足条件的有2个；
当OA是腰，O是顶角顶点时，B是以O为圆心，以OA为半径的圆与坐标轴的交点，共有4个点；
当OA是腰，A是顶角顶点时，B是以A为圆心，以OA为半径的圆与坐标轴的交点，除去原点O以外有2个点．
则满足条件的点有：2+4+2=8个．
其中横纵坐标均为整数的有2个，
故答案为8，2．
解：当OA是底边时，B在线段OA的中垂线上，与坐标轴有2个交点，则满足条件的有2个；当OA是腰，O是顶角顶点时，B是以O为圆心，以OA为半径的圆与坐标轴的交点，共有4个点；
当OA是腰，A是顶角顶点时，B是以A为圆心，以OA为半径的圆与坐标轴的交点，除去原点O以外有2个点．
则满足条件的点有：2+4+2=8个．
其中横纵坐标均为整数的有2个，
故答案为8，2．
点评：本题主要考查了等腰三角形的判定，正确根据等腰三角形的定义进行分类讨论是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
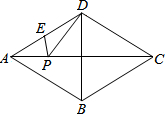已知四边形ABCD为菱形，∠BAD=60°，E为AD中点，AB=6cm，P为AC上任一点．求PE+PD的最小值是
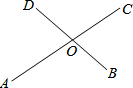如图，AC、BD是相交的两条线段，O分别为它们的中点．当BD绕点O旋转时，连接AB、BC、CD、DA所得到的四边形ABCD始终为
如图四边形ABCD中EF∥AD，MN∥AB，MN与EF交于点P且点P在BD上，图中面积相等的四边形有
如图，在?ABCD中，若BE平分∠ABC，求ED．