题目内容
已知﹙a，0﹚，﹙b，0﹚为抛物线y=﹙x-c﹚﹙x-c-d﹚-2与x轴的两个交点，且﹙a，0﹚在﹙b，0﹚的左边，求代数式|a-c|-|c-b|的值．
考点：抛物线与x轴的交点
专题：计算题
分析：先画出y=（x-c）（x-c-d）的图象，再根据y=（x-c）（x-c-d）-2的图象是由y=（x-c）（x-c-d）的图象向下移动2个单位得到的，得出a＜c＜b，再把代数式|a-c|-|c-b|化简即可．
解答：
解：∵y=（x-c）（x-c-d）-2的图象是将y=（x-c）（x-c-d）的图象向下移动2个单位得到的，
∴a＜c＜b，
∴a-c＜0，c-b＜0，
∴|a-c|-|c-b|=c-a+c-b=2c-a-b．
解：∵y=（x-c）（x-c-d）-2的图象是将y=（x-c）（x-c-d）的图象向下移动2个单位得到的，∴a＜c＜b，
∴a-c＜0，c-b＜0，
∴|a-c|-|c-b|=c-a+c-b=2c-a-b．
点评：此题考查了抛物线与x轴的交点问题，用到的知识点是抛物线与x轴的交点坐标，关键是根据二次函数图象的移动规律和抛物线与x轴的交点坐标得出a＜c＜b．
练习册系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
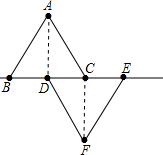在直角坐标中，有两个边长都为10cm的等边三角形△ABC和△DEF，且BC、DE与x轴重合，B与原点O重合，连结AD、CF．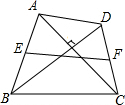
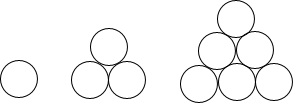瓶子或罐头盒等物体常如下图那样堆放，试确定瓶子总数y与层数x之间的关系式，并写出自变量x的取值范围．
如图，在矩形ABCD中，AB=4，AD=5，P是射线BC上的一个动点，过点P作PE⊥AP，交射线DC于点E，射线AE交射线BC于点F，设BP=a．