题目内容
已知抛物线y=ax2-1与x轴交于点A(-1,0),与y轴交于点B,点P是抛物线上的一点,若△PAB是直角三角形,则点P的坐标为 .
考点:抛物线与x轴的交点
专题:代数几何综合题,分类讨论
分析:把点A(-1,0)代入抛物线y=ax2-1得抛物线的解析式为;y=x2-1,再求出点B、C的坐标,再证出∠CBA=90°,得出点P在点C处时,△PAB是直角三角形,求出点P的坐标,过点A作PA⊥AB,交y轴与点D,求出直线AC的解析式为;y=x+1,再由
即可求出点P的坐标.
|
解答:解:把点A(-1,0)代入抛物线y=ax2-1得;0=a-1,a=1,
则抛物线的解析式为;y=x2-1,点B的坐标为(0,-1),
设抛物线y=ax2-1与x轴的另一个交点为C,则点C的坐标为(1,0),
∵OB=OC=1,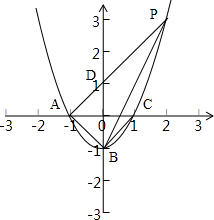
∴∠OBC=45°,
∵OB=OA,
∴∠OBA=45°,
∴∠CBA=90°,
∴点P在点C处时,△PAB是直角三角形,点P的坐标为(1,0),
过点A作PA⊥AB,交y轴与点D,
∵∠OAB=45°,
∴∠OAD=∠ODA=45°,
∴OA=OD=1,
∴点D的坐标为(0,1),
∴直线AC的解析式为;y=x+1,
由
得:
(舍去),
,
∴点P的坐标为(2,3);
故答案为;(1,0),(2,3).
则抛物线的解析式为;y=x2-1,点B的坐标为(0,-1),
设抛物线y=ax2-1与x轴的另一个交点为C,则点C的坐标为(1,0),
∵OB=OC=1,

∴∠OBC=45°,
∵OB=OA,
∴∠OBA=45°,
∴∠CBA=90°,
∴点P在点C处时,△PAB是直角三角形,点P的坐标为(1,0),
过点A作PA⊥AB,交y轴与点D,
∵∠OAB=45°,
∴∠OAD=∠ODA=45°,
∴OA=OD=1,
∴点D的坐标为(0,1),
∴直线AC的解析式为;y=x+1,
由
|
|
|
∴点P的坐标为(2,3);
故答案为;(1,0),(2,3).
点评:此题考查了抛物线与x轴的交点,用到的知识点是抛物线与坐标轴的交点、一次函数与抛物线的交点,关键是根据题意画出图形,要注意分两种情况求解.

练习册系列答案
相关题目
在梯形ABCD中,AD∥BC,∠B=90°,AB=12,BC=10,AD=5,则CD的长是( )
| A、13 | B、14 | C、15 | D、16 |
 如图,在矩形ABCD中,AB=4,AD=5,P是射线BC上的一个动点,过点P作PE⊥AP,交射线DC于点E,射线AE交射线BC于点F,设BP=a.
如图,在矩形ABCD中,AB=4,AD=5,P是射线BC上的一个动点,过点P作PE⊥AP,交射线DC于点E,射线AE交射线BC于点F,设BP=a.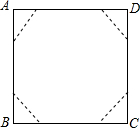 如图,将一边长为1的正方形硬纸板剪去四个角,使它变为正八边形,求这个正八边形的面积.
如图,将一边长为1的正方形硬纸板剪去四个角,使它变为正八边形,求这个正八边形的面积.