题目内容
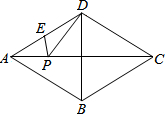已知四边形ABCD为菱形，∠BAD=60°，E为AD中点，AB=6cm，P为AC上任一点．求PE+PD的最小值是考点：轴对称-最短路线问题,菱形的性质
专题：几何图形问题
分析：根据菱形的性质，可得AC是BD的垂直平分线，可得AC上的点到D、B点的距离相等，连接BE交AC与P，可得答案．
解答：解：∵菱形的性质，
∴AC是BD的垂直平分线，AC上的点到B、D的距离相等．
连接BE交AC于P点，
PD=PB，
PE+PD=PE+PB=BE，
在Rt△ABE中，由勾股定理得
BE=
=
=3
，
故答案为：3
．
∴AC是BD的垂直平分线，AC上的点到B、D的距离相等．
连接BE交AC于P点，
PD=PB，
PE+PD=PE+PB=BE，
在Rt△ABE中，由勾股定理得
BE=
| AB2-AE2 |
| 62-32 |
| 3 |
故答案为：3
| 3 |
点评：本题考查了轴对称，对称轴上的点到线段两端点的距离相等是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在矩形ABCD中，AB=4，AD=5，P是射线BC上的一个动点，过点P作PE⊥AP，交射线DC于点E，射线AE交射线BC于点F，设BP=a．
如图，已知在△ABC中，∠C=90°，AD是角平分线，过点B作BA的垂线与AD的延长线相交于点E，求证：△BDE是等腰三角形．