题目内容
 如图,B处在A处的南偏西60°方向,C处在A处的南偏东20°方向,C处在B处南的偏东80°方向,求∠ACB.
如图,B处在A处的南偏西60°方向,C处在A处的南偏东20°方向,C处在B处南的偏东80°方向,求∠ACB.分析:首先根据方向角的定义,求得∠BAC的度数,以及∠ABG的度数,则∠AGB的度数即可求得,然后在△BCG中,利用外角的性质定理即可求解.
解答: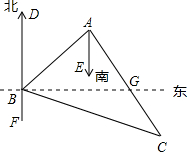 解:∵∠BAE=60°,∠EAC=20°,
解:∵∠BAE=60°,∠EAC=20°,
∴∠BAC=60°+20°=80°,∠ABG=30°
∵∠FBC=80°,
∴∠GBC=90-80=10°,
∴∠AGB=180°-30°-80°=70°,
∴∠ACB=∠AGB-∠GBC=70°-10°=60°.
 解:∵∠BAE=60°,∠EAC=20°,
解:∵∠BAE=60°,∠EAC=20°,∴∠BAC=60°+20°=80°,∠ABG=30°
∵∠FBC=80°,
∴∠GBC=90-80=10°,
∴∠AGB=180°-30°-80°=70°,
∴∠ACB=∠AGB-∠GBC=70°-10°=60°.
点评:本题考查了方向角的定义以及三角形的外角的性质,正确理解方向角的定义是关键.

练习册系列答案
相关题目
 17、如图,B处在A处的南偏西50°的方向,C处在A处的南偏东15°的方向,C处在B处的北偏东84°的方向.求∠C的度数.
17、如图,B处在A处的南偏西50°的方向,C处在A处的南偏东15°的方向,C处在B处的北偏东84°的方向.求∠C的度数. 19、如图,B处在A处的南偏西57°的方向,C处在A处的南偏东15°方向,C处在B处的北偏东82°方向.求∠C的度数.
19、如图,B处在A处的南偏西57°的方向,C处在A处的南偏东15°方向,C处在B处的北偏东82°方向.求∠C的度数.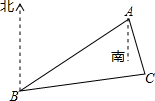 如图,B处在A处的南偏西56°的方向,C处在A处的南偏东16°方向,C处在B处的北偏东82°方向.∠C的度数为
如图,B处在A处的南偏西56°的方向,C处在A处的南偏东16°方向,C处在B处的北偏东82°方向.∠C的度数为 如图,B处在A处的南偏西80°方向,C处在A处的南偏西45°方向,C处在B处的南偏东20°方向,求∠ACB.
如图,B处在A处的南偏西80°方向,C处在A处的南偏西45°方向,C处在B处的南偏东20°方向,求∠ACB.