题目内容
【题目】将一个正方形纸片AOBC放置在平面直角坐标系中,点A(0,4),点O(0,0),B(4,0),C(4,4)点.动点E在边AO上,点F在边BC上,沿EF折叠该纸片,使点O的对应点M始终落在边AC上(点M不与A,C重合),点B落在点N处,MN与BC交于点P.
(Ⅰ)如图①,当∠AEM=30°时,求点E的坐标;
(Ⅱ)如图②,当点M落在AC的中点时,求点E的坐标;
(Ⅲ)随着点M在AC边上位置的变化,△MPC的周长是否发生变化?如变化,简述理由;如不变,直接写出其值.
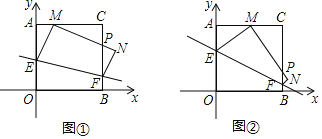
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)△MPC的周长不变,为8,理由见解析
;(Ⅲ)△MPC的周长不变,为8,理由见解析
【解析】
(Ⅰ)由折叠的性质知OE=EM,设OE=x,则EM=OE=x,AE=![]() x,根据等量关系AE+OE=OA列出方程并解答;
x,根据等量关系AE+OE=OA列出方程并解答;
(Ⅱ)由线段中点的定义知AM=![]() AC=2.设OE=m,则EM=OE=m,AE=4﹣m,在Rt△AEM中,由勾股定理列出关于x的方程并解答;
AC=2.设OE=m,则EM=OE=m,AE=4﹣m,在Rt△AEM中,由勾股定理列出关于x的方程并解答;
(Ⅲ)设AM=a,则OE=EM=b,MC=4﹣a,在Rt△AEM中,由勾股定理得出a、b的关系式,可证Rt△AEM∽Rt△CMP,根据相似三角形的周长比等于相似比求△MPC的周长.
解:(Ⅰ)如图①,
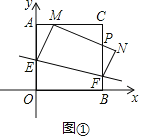
∵四边形ABCD是正方形,
∴∠EAM=90°.
由折叠知OE=EM.
设OE=x,则EM=OE=x,
在Rt△AEM中,cos∠AEM=![]()
∵∠AEM=30°
∴cos30°=![]() =
=![]()
∴AE=![]() x,
x,
∴AE+OE=OA,即![]() x+x=4,
x+x=4,
∴x=16﹣8![]() .
.
∴![]()
(Ⅱ)如图②,
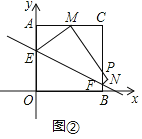
∵点M是边AC的中点,
∴AM=![]() AC=2.
AC=2.
设OE=m,则EM=OE=m,AE=4﹣m,
在Rt△AEM中,EM2=AM2+AE2,
即m 2=22+(4﹣m)2,解得m=![]() .
.
∴![]() ;
;
(Ⅲ)△MPC的周长不变,为8.
理由:设AM=a,OE=EM=b,
∵AC=4
∴MC=4﹣a,
在Rt△AEM中,由勾股定理得AE2+AM2=EM2,
(4﹣b)2+a2=b2,解得16+a2=8b.
∴16﹣a2=8(4﹣b)
∵∠EMP=90°,∠A=∠C,
∴Rt△AEM∽Rt△CMP,
∴![]() ,即
,即![]() ,
,
解得DM+MP+DP=![]() =8.
=8.
∴△CMP的周长为8.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案【题目】近一周,各个学校均在紧张有序地进行中考模拟考试,学生们通过模拟考试来调整自己的状态并了解自己的学业水平.某中学物理教研组想通过此次中考模拟的成绩来预估中考的各个分数段人数,在全年级随机抽取了男.女各40名学生的成绩(满分为80分,女生成绩中最低分为45分),并将数据进行整理分析,给出了下面部分信息:
①男生成绩扇形统计图和女生成绩频数分布直方图如下:(数据分组为A组:x<50;B组:50≤x<60;C组:60≤x<70;D组:70≤x≤80)

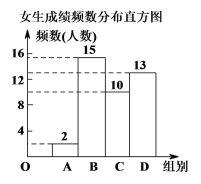
②男生C组中全部15名学生的成绩为:
63,69,64,62,68,69,65,69,65,66,67,61,67,66,69.
③两组数据的平均数.中位数.众数.满分率.极差(单位:分)如下表所示:
平均数 | 中位数 | 众数 | 满分率 | 极差 | |
男生 | 70 | b | c | 25% | 32 |
女生 | 70 | 68 | 78 | 15% | d |
(1)扇形统计图A组学生中所对应的圆心角α的度数为 ,中位数b= ,众数c= ,极差d= .
(2)通过以上的数据分析,你认为 (填“男生”或“女生”)的物理成绩更好,并说明理由:
① ;② .
(3)若成绩在70分(包含70分)以上为优秀,请你估计该校1200名学生中此次考试中优秀的人数.