题目内容
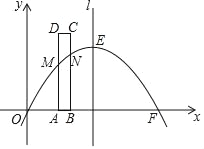
【题目】如图,已知抛物线y=ax2+bx与x轴分别交于原点O和点F(10,0),与对称轴l交于点E(5,5).矩形ABCD的边AB在x轴正半轴上,且AB=1,边AD,BC与抛物线分别交于点M,N.当矩形ABCD沿x轴正方向平移,点M,N位于对称轴l的同侧时,连接MN,此时,四边形ABNM的面积记为S;点M,N位于对称轴l的两侧时,连接EM,EN,此时五边形ABNEM的面积记为S.将点A与点O重合的位置作为矩形ABCD平移的起点,设矩形ABCD平移的长度为t(0≤t≤5).
(1)求出这条抛物线的表达式;
(2)当t=0时,求S△OBN的值;
(3)当矩形ABCD沿着x轴的正方向平移时,求S关于t(0<t≤5)的函数表达式,并求出t为何值时,S有最大值,最大值是多少?
【答案】(1)抛物线的表达式为y=﹣![]() x2+2x;(2)
x2+2x;(2)![]() ;
;
(3)S=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() (0<t≤4);S=﹣
(0<t≤4);S=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() (4<t≤5),当t=
(4<t≤5),当t=![]() 时,S有最大值,最大值是
时,S有最大值,最大值是![]() .
.
【解析】
(1)将E(5,5)、F(10,0)代入y=ax2+bx,求解即可得到答案;
(2)当t=0时,点B的坐标为(1,0),点N的坐标为(1,![]() ),然后根据三角形的面积公式计算即可;
),然后根据三角形的面积公式计算即可;
(3)①当0<t≤4时(图1),S为梯形ABNM的面积,用t表示出各点的坐标,然后根据梯形面积公式得到关于t的二次函数,再利用二次函数的性质求得S的最大值;
②当4<t≤5时(图2),S为五边形ABNEM的面积,即两个梯形相加,同①求得S的最大值,与①所得S进行比较,较大的即为所求.
(1)将E(5,5)、F(10,0)代入y=ax2+bx,
![]() ,
,
解得: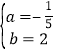 ,
,
∴抛物线的表达式为y=﹣![]() x2+2x;
x2+2x;
(2)当t=0时,点B的坐标为(1,0),点N的坐标为(1,![]() ),
),
∴BN=![]() ,OB=1,
,OB=1,
∴S△OBN=![]() BNOB=
BNOB=![]() ;
;
(3)①当0<t≤4时(图1),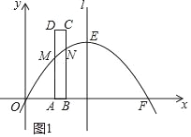
点A的坐标为(t,0),点B的坐标为(t+1,0),
∴点M的坐标为(t,﹣![]() t2+2),点N的坐标为(t+1,﹣
t2+2),点N的坐标为(t+1,﹣![]() (t+1)2+2(t+1)),
(t+1)2+2(t+1)),
∴AM=﹣![]() t2+2t,BN=﹣
t2+2t,BN=﹣![]() (t+1)2+2(t+1),
(t+1)2+2(t+1),
∴S=![]() (AM+BN)AB=
(AM+BN)AB=![]() ×1×[﹣
×1×[﹣![]() t2+2t﹣
t2+2t﹣![]() (t+1)2+2(t+1)],
(t+1)2+2(t+1)],
=﹣![]() t2+
t2+![]() t+
t+![]() ,
,
=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∵﹣![]() <0,
<0,
∴当t=4时,S取最大值,最大值为![]() ;
;
②当4<t≤5时(图2),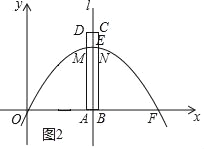
点A的坐标为(t,0),点B的坐标为(t+1,0),
∴点M的坐标为(t,﹣![]() t2+2t),点N的坐标为(t+1,﹣
t2+2t),点N的坐标为(t+1,﹣![]() (t+1)2+2(t+1)),
(t+1)2+2(t+1)),
∴AM=﹣![]() t2+2t,BN=﹣
t2+2t,BN=﹣![]() (t+1)2+2(t+1),
(t+1)2+2(t+1),
∴S=![]() (5﹣t)(﹣
(5﹣t)(﹣![]() t2+2t+5)+
t2+2t+5)+![]() (t﹣4)[5﹣
(t﹣4)[5﹣![]() (t+1)2+2(t+1)],
(t+1)2+2(t+1)],
=![]() (
(![]() t3﹣3t2+5t+25)+
t3﹣3t2+5t+25)+![]() (﹣
(﹣![]() t3+
t3+![]() t2+
t2+![]() t﹣
t﹣![]() ),
),
=﹣![]() t2+
t2+![]() t﹣
t﹣![]() ,
,
=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∵﹣![]() <0,
<0,
∴当t=![]() 时,S取最大值,最大值为
时,S取最大值,最大值为![]() ;
;
∵![]() =
=![]() <
<![]() ,
,
∴当t=![]() 时,S有最大值,最大值是
时,S有最大值,最大值是![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案