题目内容
如图,抛物线y=ax2-3x+c交x轴正方向于A、B两点,交y轴正方向于C点,过A、B、C三点作⊙D.若⊙D与y轴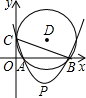 相切.
相切.(1)求a、c满足的关系式;
(2)设∠ACB=a,求tana;
(3)设抛物线顶点为P,判断直线PA与⊙D的位置关系.
分析:(1)由题意,抛物线y=ax2-3x+c交x轴正方向于A、B两点,即A、B的横坐标是方程ax2-3x+c=0的两根,再由圆的切割线定理,易求a,c的关系;
(2)作辅助线,连接PD,交x轴于E,连接AD、BD,根据几何关系求出AE,DE的关系,从而求出tana的值;
(3)连接PA,求出P点坐标,在Rt△PAE中,求出β的正切值,从而判断直线PA与⊙D的位置关系.
(2)作辅助线,连接PD,交x轴于E,连接AD、BD,根据几何关系求出AE,DE的关系,从而求出tana的值;
(3)连接PA,求出P点坐标,在Rt△PAE中,求出β的正切值,从而判断直线PA与⊙D的位置关系.
解答:解:(1)由题意,抛物线y=ax2-3x+c交x轴正方向于A、B两点,
∴A、B的横坐标是方程ax2-3x+c=0的两根,
设为x1、x2(x2>x1),C的纵坐标是c,
又∵y轴与⊙D相切,
∴OA•OB=OC2.
∴x1•x2=c2
又由方程ax2-3x+c=0,知x1•x2=
∴c2=
,即ac=1;
(2)连接PD,交x轴于E,直线PD必为抛物线的对称轴,连接AD、BD,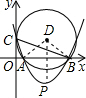
∴AE=
AB,∠ACB=
∠ADB=∠ADE=a,
∵a>0,x2>x1,
∴AB=x2-x1=
,
∴AE=
,
又ED=OC=c,
∴tana=
=
;
(3)设∠PAB=β,
∵P点坐标为(
,-
)且a>0,
∴在Rt△PAE中,PE=
,
∴tanβ=
=
,
∴tanβ=tanα,
∴β=α,
∴∠PAE=∠ADE,
∵∠ADE+∠DAE=90°,
∴∠PAE+∠DAE=90°,
即∠PAD=90°,
∴PA和⊙D相切.
∴A、B的横坐标是方程ax2-3x+c=0的两根,
设为x1、x2(x2>x1),C的纵坐标是c,
又∵y轴与⊙D相切,
∴OA•OB=OC2.
∴x1•x2=c2
又由方程ax2-3x+c=0,知x1•x2=
| c |
| a |
∴c2=
| c |
| a |
(2)连接PD,交x轴于E,直线PD必为抛物线的对称轴,连接AD、BD,

∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
∵a>0,x2>x1,
∴AB=x2-x1=
| ||
| a |
∴AE=
| ||
| 2a |
又ED=OC=c,
∴tana=
| AE |
| DE |
| ||
| 2 |
(3)设∠PAB=β,
∵P点坐标为(
| 3 |
| 2a |
| 5 |
| 4a |
∴在Rt△PAE中,PE=
| 5 |
| 4a |
∴tanβ=
| PE |
| AE |
| ||
| 2 |
∴tanβ=tanα,
∴β=α,
∴∠PAE=∠ADE,
∵∠ADE+∠DAE=90°,
∴∠PAE+∠DAE=90°,
即∠PAD=90°,
∴PA和⊙D相切.
点评:此题考查了二次函数的基本性质和圆与直线的位置关系,把函数与方程联系起来,把圆与抛物线联系起来,主要运用圆的切割线定理,直角三角形的勾股定理,用的知识点多较为复杂.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少? O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).