Question

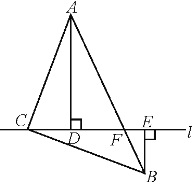
【题目】如图，直角三角形与直角三角形的斜边在同一直线上，，，平分，将绕点按逆时针方向旋转，记为，在旋转过程中：

（1）如图，当______时，，当______时，；

（2）如图，当顶点在内部时，边、分别交、的延长线于点、，记，．

①与度数的和是否变化？若不变，求出与度数和；若变化，请说明理由；

②若使得，求出、的度数，并直接写出此时的度数．

Answer 1

【答案】(1)10°，100°；(2)①不变，详见解析；②80°．

【解析】

(1)当∠EDA＝∠B＝40°时，DE∥BC，得出 30°+α＝40°，即可得出结果；当 DE∥AC 时，DE⊥AB，得出 50°+α+30°＝180°，即可得出结果；

(2)①连接 MN，由三角形内角和定理得出∠CNM+∠CMN+∠MCN＝180°，则∠CNM+∠CMN＝90°，由三角形内角和定理得出∠DNM+∠DMN+∠MDN＝180°，即∠2+∠CNM+∠CMN+∠1+∠MDN＝180°，即可得出结论；②根据①中结论结合本题题意可以得出度数，即可求出度数．

解：（1）∵∠B＝40°，

∴当∠EDA＝∠B＝40°时，DE∥BC， 而∠EDF＝30°，

∴30°+α＝40°，

解得：α＝10°；

当 DE∥AC 时，DE⊥AB， 此时∠A+∠EDA＝180°， ∠A＝90°－∠B＝50°，

∴50°+α+30°＝180°， 解得：α＝100°；

故答案为 10°，100°；

（2）①∠1 与∠2 度数的和不变；理由如下：

连接 MN，如图所示：

在△CMN 中，∵∠CNM+∠CMN+∠MCN＝180°，

∴∠CNM+∠CMN＝90°， 在△MND 中，

∵∠DNM+∠DMN+∠MDN＝180°， 即∠2+∠CNM+∠CMN+∠1+∠MDN＝180°，

∴∠1+∠2＝180°－90°－30°＝60°．

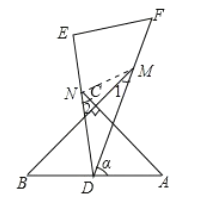
②∵，

∴，．

∴．