题目内容
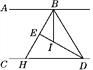
【题目】如图,已知BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°.
(1)试说明:AB∥CD;
(2)H是BE的延长线与直线CD的交点,BI平分∠HBD,写出∠EBI与∠BHD的数量关系,并说明理由.
【答案】(1)详见解析;(2)∠EBI=![]() ∠BHD,理由详见解析.
∠BHD,理由详见解析.
【解析】试题分析:(1)根据角平分线的定义可得∠ABD=2∠EBD,∠BDC=2∠BDE,然后求出∠ABD+∠BDC=180°,再根据同旁内角互补,两直线平行证明;
(2)由AB∥CD,得到∠ABH=∠BHD,再由BI平分∠EBD,BH平分∠ABD,即可得出结论.
试题解析:
(1)证明:∵BE平分∠ABD,DE平分∠BDC,
∴∠ABD=2∠EBD,∠BDC=2∠BDE,
∵∠EBD+∠EDB=90°,
∴∠ABD+∠BDC=2×90°=180°,
∴AB∥CD;
(2)∠EBI=![]() ∠BHD. 理由如下:
∠BHD. 理由如下:
因为AB∥CD,
所以∠ABH=∠BHD.
因为BI平分∠EBD,BH平分∠ABD,
所以∠EBI=![]() ∠EBD=
∠EBD=![]() ∠ABH=
∠ABH=![]() ∠BHD.
∠BHD.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目