题目内容
【题目】已知,△ABC中,AC=BC,∠ACB=90°,D为AB的中点,若E在直线AC上任意一点,DF⊥DE,交直线BC于F点.G为EF的中点,延长CG交AB于点H. 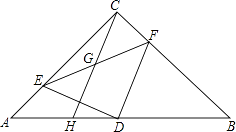
(1)若E在边AC上. ①试说明DE=DF;
②试说明CG=GH;
(2)若AE=3,CH=5.求边AC的长.
【答案】
(1)解:①连接CD,
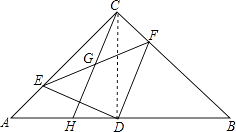
∵∠ACB=90°,D为AB的中点,AC=BC,
∴CD=AD=BD,
又∵AC=BC,
∴CD⊥AB,
∴∠EDA+∠EDC=90°,∠DCF=∠DAE=45°,
∵DF⊥DE,
∴∠EDF=∠EDC+∠CDF=90°,
∴∠ADE=∠CDF,
在△ADE和△CDF中
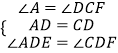
∴△ADE≌△CDF,
∴DE=DF.
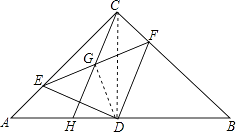
②连接DG,
∵∠ACB=90°,G为EF的中点,
∴CG=EG=FG,
∵∠EDF=90°,G为EF的中点,
∴DG=EG=FG,
∴CG=DG,
∴∠GCD=∠CDG
又∵CD⊥AB,
∴∠CDH=90°,
∴∠GHD+∠GCD=90°,∠HDG+∠GDC=90°,
∴∠GHD=∠HDG,
∴GH=GD,
∴CG=GH.
(2)解:如图,当E在线段AC上时,

∵CG=GH=EG=GF,
∴CH=EF=5,
∵△ADE≌△CDF,
∴AE=CF=3,
∴在Rt△ECF中,由勾股定理得: ![]() ,
,
∴AC=AE+EC=3+4=7;
如图,当E在线段CA延长线时,
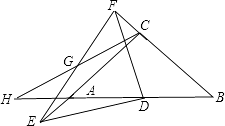
AC=EC﹣AE=4﹣3=1,
综合上述AC=7或1.
【解析】(1)①连接CD,推出CD=AD,∠CDF=∠ADE,∠A=∠DCB,证△ADE≌△CDF即可;②连接DG,根据直角三角形斜边上中线求出CG=EG=GF=DG,推出∠GCD=∠GDC,推出∠GDH=∠GHD,推出DG=GH即可;(2)求出EF=5,根据勾股定理求出EC,即可得出答案.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目