Question

【题目】（本题10分）对于平面直角坐标系xOy中的点P(a，b)，若点P的坐标为(a＋，ka＋b)（k为常数，k≠0），则称点P′为点P的“k属派生点”．例如：P(1，4)的“2属派生点”为P′(1＋，2×1＋4)，即P′(3，6).

(1) ① 点P(－1，－2)的“2属派生点”P′的坐标为_______________

② 若点P的“k属派生点”为P′(3，3)，请写出一个符合条件的点P的坐标_____________

(2) 若点P在x轴的正半轴上，点P的“k属派生点”为P′点，且△OPP′为等腰直角三角形，则k的值为____________

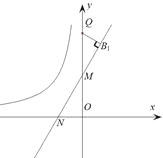
(3) 如图，点Q的坐标为(0， )，点A在函数（x＜0）的图象上，且点A是点B的“属派生点”．当线段BQ最短时，求B点坐标.

Answer 1

【答案】（1）①；②（1，2）（答案不唯一）；（2）；（3）.

【解析】试题分析：（1）①根据派生点的定义，点P的“2属派生点” 的坐标为（， ），即.

②答案不唯一，只需横、纵坐标之和为3即可，如（1，2）.

（2）若点P在x轴的正半轴上，则P（a，0），点P的“k属派生点”为点为（， ）.

∵且△为等腰直角三角形，∴.

（3）求出点B所在的直线，根据垂直线段最短的性质即可求得B点坐标.

试题解析：（1）①.

②．（1，2）.

（2）.

（3）设B（a，b）.

∵B的“属派生点”是A，∴.

∵点A还在反比例函数的图象上，

∴．∴.

∵，∴．∴.

∴B在直线上.

过Q作的垂线QB1,垂足为B1，

∵，且线段BQ最短，∴B1即为所求的点B．

∴易求得.