题目内容
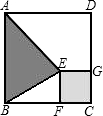 如图,在一块正方形ABCD木板上要贴三种不同的墙纸,正方形EFCG部分贴A型墙纸,△ABE部分贴B型墙纸,其余部分贴C型墙纸.A型、B型、C型三种墙纸的单价分别为每平方60元、80元、40元.
如图,在一块正方形ABCD木板上要贴三种不同的墙纸,正方形EFCG部分贴A型墙纸,△ABE部分贴B型墙纸,其余部分贴C型墙纸.A型、B型、C型三种墙纸的单价分别为每平方60元、80元、40元.探究1:如果木板边长为2米,FC=1米,则一块木板用墙纸的费用需
探究2:如果木板边长为1米,求一块木板需用墙纸的最省费用.
分析:(1)首先求出正方形EGFC和三角形ABE的面积,再求出剩余的面积,用个面积乘以所需费用,
(2)设EF=x,BF=(1-x)m,总费用为y元,用x表示出正方形EGFC和三角形ABE的面积,用x表示总费用,求出其最值.
(2)设EF=x,BF=(1-x)m,总费用为y元,用x表示出正方形EGFC和三角形ABE的面积,用x表示总费用,求出其最值.
解答:解:(1)正方形EGFC的面积=1,三角形ABE的面积为1,空白面积为2,总费用=1×60+1×80+2×40=220元;
(2)设EF=xm,BF=(1-x)m,总费用为y元,
正方形EGFC的面积=x2,△ABE的面积=
,
空白面积为:1-x2-
,
故总费用:y=60x2+80(
)+40(1-x2-
),即y=20x2-20x+60=20(x-
)2+55,
当x=
时,y最小=55元.
(2)设EF=xm,BF=(1-x)m,总费用为y元,
正方形EGFC的面积=x2,△ABE的面积=
| 1-x |
| 2 |
空白面积为:1-x2-
| 1-x |
| 2 |
故总费用:y=60x2+80(
| 1-x |
| 2 |
| 1-x |
| 2 |
| 1 |
| 2 |
当x=
| 1 | ||||
|
点评:本题主要考查二次函数的应用,列出面积和边长之间的函数关系式是解题的关键,运用二次函数解决实际问题,比较简单.

练习册系列答案
相关题目
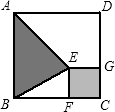 分贴C型墙纸.A型、B型、C型三种墙纸的单价分别为每平方60元、80元、40元.
分贴C型墙纸.A型、B型、C型三种墙纸的单价分别为每平方60元、80元、40元. 如图,在一块正方形的木板上可以截出最大的圆的面积为3π,求正方形木板的边长.
如图,在一块正方形的木板上可以截出最大的圆的面积为3π,求正方形木板的边长.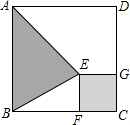 如图,在一块正方形ABCD木板上要贴三种不同的墙纸,正方形EFCG部分贴A型墙纸,△ABE部分贴B型墙纸,其余部分贴C型墙纸.A型、B型、C型三种墙纸的单价分别为每平方60元、80元、40元.
如图,在一块正方形ABCD木板上要贴三种不同的墙纸,正方形EFCG部分贴A型墙纸,△ABE部分贴B型墙纸,其余部分贴C型墙纸.A型、B型、C型三种墙纸的单价分别为每平方60元、80元、40元.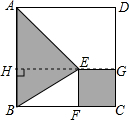 型墙纸,其余部分贴C型墙纸.A型、B型、C型三种墙纸的单价分别为每平方米60元、80元、40元.
型墙纸,其余部分贴C型墙纸.A型、B型、C型三种墙纸的单价分别为每平方米60元、80元、40元.