题目内容
【题目】已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.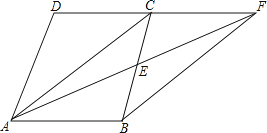
【答案】解:四边形ABFC是平行四边形;理由如下:
∵AB∥CD,
∴∠BAE=∠CFE,
∵E是BC的中点,
∴BE=CE,
在△ABE和△FCE中, 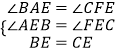 ,
,
∴△ABE≌△FCE(AAS);
∴AE=EF,
又∵BE=CE
∴四边形ABFC是平行四边形
【解析】利用平行线的性质得出∠BAE=∠CFE,由AAS得出△ABE≌△FCE,得出对应边相等AE=EF,再利用平行四边形的判定得出即可.此题主要考查了平行四边形的判定、全等三角形的判定与性质等知识;熟练掌握平行四边形的判定方法,证明三角形全等是解决问题的关键.
【考点精析】本题主要考查了平行四边形的判定的相关知识点,需要掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形才能正确解答此题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目