��Ŀ����
��ͼ����Rt��ABC�У�AB=AC��P�DZ�AB�������˵㣩�ϵĶ��㣬��P��BC�Ĵ���PR��RΪ���㣬��PRB��ƽ������AB�ཻ�ڵ�S����֪���߶�RS�ϴ���һ��T�������߶�PTΪһ����������PTEF���䶥��E��Fǡ�÷ֱ��ڱ�BC��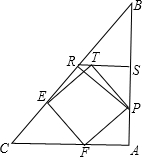 AC�ϣ�
AC�ϣ���1��֤������SBR�ס�ABC��
��2��֤����ST=AP��
��3����AB=1��PA=x��������PTEF�����Ϊy������y��x�ĺ�����ϵ�������x��ȡֵ��Χ��
��������1��������PR��BC��RS�ǡ�PRB��ƽ���ߣ���֤��ABC�ǵ���ֱ�������Σ����֤�á�BRS=45��=��C�����������Ƕ�Ӧ��ȵ����������ƣ�����֤�ã���SBR�ס�ABC��
��2������AAS����֤�á�SPT�ա�AFP������ȫ�������εĶ�Ӧ����ȣ�����֤��ST=AP��
��3����������ֱ���ã�BS��PS��ST��AP��ֵ�����ɹ��ɶ����������������PTEF���������ST��SP���������x��ȡֵ��Χ��
��2������AAS����֤�á�SPT�ա�AFP������ȫ�������εĶ�Ӧ����ȣ�����֤��ST=AP��
��3����������ֱ���ã�BS��PS��ST��AP��ֵ�����ɹ��ɶ����������������PTEF���������ST��SP���������x��ȡֵ��Χ��
��� ��1��֤������PR��BC��RS�ǡ�PRB��ƽ���ߣ�
��1��֤������PR��BC��RS�ǡ�PRB��ƽ���ߣ�
���BRS=45�㣬
�ߡ�ABC�ǵ���ֱ�������Σ�
���BRS=45��=��C����B=��B��
���SBR�ס�ABC��
��2��֤�����ڡ�SPT�͡�AFP�У�
��TP=PF��
�ɣ�1��֪����PST=��FAP=90�㣬
�֡ߡ�SPT+��APF=��APF+��AFP=90�㣬
���SPT=��AFP��
���SPT�ա�AFP��
��ST=AP��
��3���⣺��AP=x��
��BS=PS=
��
�ɣ�2��֪��ST=AP=x��
��������PTEF�����y=PT2=PS2+ST2=��
��2+x2=
x2-
x+
��
��ͼ֪��ST��SP����x��
��
��x��
��
��x��ȡֵ��Χ�ǣ�0��x��
��
 ��1��֤������PR��BC��RS�ǡ�PRB��ƽ���ߣ�
��1��֤������PR��BC��RS�ǡ�PRB��ƽ���ߣ����BRS=45�㣬
�ߡ�ABC�ǵ���ֱ�������Σ�
���BRS=45��=��C����B=��B��
���SBR�ס�ABC��
��2��֤�����ڡ�SPT�͡�AFP�У�
��TP=PF��
�ɣ�1��֪����PST=��FAP=90�㣬
�֡ߡ�SPT+��APF=��APF+��AFP=90�㣬
���SPT=��AFP��
���SPT�ա�AFP��
��ST=AP��
��3���⣺��AP=x��
��BS=PS=
| 1-x |
| 2 |
�ɣ�2��֪��ST=AP=x��
��������PTEF�����y=PT2=PS2+ST2=��
| 1-x |
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
��ͼ֪��ST��SP����x��
| 1-x |
| 2 |
��x��
| 1 |
| 3 |
��x��ȡֵ��Χ�ǣ�0��x��
| 1 |
| 3 |
���������⿼����ȫ�������������������ε��ж������ʣ��Լ����ɶ�����֪ʶ���ۺ�Ӧ�ã���Ŀ�Ѷ����У�ע�����ν��˼���Ӧ�ã�

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
 ��2013•�����ʼ죩��ͼ����Rt��ABC�У���C=90�㣬��BAC��ƽ����AD��BC�ڵ�D����E��AB��һ�㣬��AEΪֱ���ġ�O����D���ҽ�AC�ڵ�F��
��2013•�����ʼ죩��ͼ����Rt��ABC�У���C=90�㣬��BAC��ƽ����AD��BC�ڵ�D����E��AB��һ�㣬��AEΪֱ���ġ�O����D���ҽ�AC�ڵ�F�� ��ͼ����Rt��ABC�У���C=90�㣬AC=6cm��BC=8cm��AD��BD�ֱ��ǡ�BAC�͡�ABC��ƽ���ߣ������ཻ�ڵ�D�����D��BC�ľ��룮
��ͼ����Rt��ABC�У���C=90�㣬AC=6cm��BC=8cm��AD��BD�ֱ��ǡ�BAC�͡�ABC��ƽ���ߣ������ཻ�ڵ�D�����D��BC�ľ��룮 �����ƶ���ʹ���30��ǵ����߷ֱ����ABC�ı�AC��BC�ཻ�ڵ�E��F����ʹDEʼ����AB��ֱ��
�����ƶ���ʹ���30��ǵ����߷ֱ����ABC�ı�AC��BC�ཻ�ڵ�E��F����ʹDEʼ����AB��ֱ�� ��ͼ����Rt��ABC�У�BD��AC��sinA=
��ͼ����Rt��ABC�У�BD��AC��sinA= ��P���A���غ�ʱ������P��PQ��AC�ڵ�Q����PQΪ����������PQMN��ʹ��M�����߶�AC�ϣ����P���˶�ʱ��Ϊt��s����
��P���A���غ�ʱ������P��PQ��AC�ڵ�Q����PQΪ����������PQMN��ʹ��M�����߶�AC�ϣ����P���˶�ʱ��Ϊt��s����