题目内容
【题目】类比等腰三角形的定义,我们定义:有三条边相等的凸四边形叫做“准等边四边形”
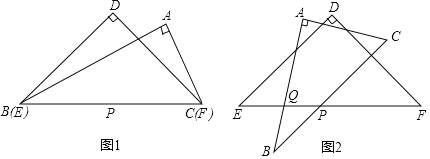
(1)已知:如图1,在“准等边四边形”ABCD中,BC≠AB,BD⊥CD,AB=3,BD=4,求BC的长;
(2)在探究性质时,小明发现一个结论:对角线互相垂直的“准等边四边形”是菱形.请你判断此结论是否正确,若正确,请说明理由;若不正确,请举出反例;
(3)如图2,在△ABC中,AB=AC,∠BAC=90°,BC=2.在AB的垂直平分线上是否存在点P使得以A,B,C,P为顶点的四边形为“准等边四边形”?若存在,请求出该“准等边四边形”的面积;若不存在,请说明理由.

【答案】(1)BC=5;(2)正确,理由见解析;(3)存在四种情况,![]() 或
或![]() +1或
+1或![]() +1或
+1或![]() 。
。
【解析】
(1)根据勾股定理计算BC的长;
(2)正确,根据对角线互相垂直平分的四边形是菱形可得结论;
(3)有四种情况:作辅助线,将四边形分成两个三角形和一个四边形或两个三角形,相加可得结论.
解:(1)如图1,Rt△ACB中,∵BD=4,CD=AB=3,
∴BC=![]() =5,
=5,
(2)正确,理由是:
如图3,AB=AD=BC,AC⊥BD,
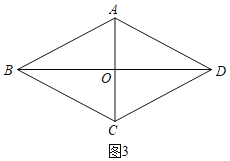
∴AO=OC,OB=OD,
∴四边形ABCD是平行四边形,
∴AB=BC,
∴ABCD是菱形;
(3)存在四种情况,
①如图2,四边形ABPC是“准等边四边形”,过C作CF⊥PE于F,则∠CFE=90°,
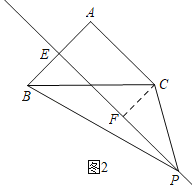
∵EP是AB的垂直平分线,
∴∠AEF=∠A=90°,
∴四边形AEFC是矩形,
Rt△ABC中,BC=2,AC=BC,
∴AC=BC=![]() ,
,
∴CF=AE=BE=![]() ,
,
∵AB=PC=![]() ,
,
∴PF=![]() =
=![]() ,
,
∴S四边形ABPC=S△BEP+S矩形AEFC+S△CFP,
=![]() ,
,
=![]() ,
,
=![]() .
.
②如图4,四边形APBC是“准等边四边形”,
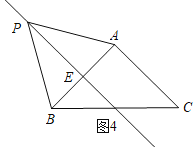
∵AP=BP=AC=![]() =AB,
=AB,
∴△ABP是等边三角形,
∴S四边形ACBP=S△APB+S△ABC=![]() +
+![]() =
=![]() +1;
+1;
③如图5,四边形ACBP是“准等边四边形”,
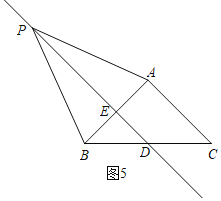
∵AP=BP=BC=2,
∵PE是AB的垂直平分线,
∴PD⊥AB,E是AB的中点,
∴BE=![]() AB=
AB=![]() ,
,
∴PE=![]() =
=![]() =
=![]() ,
,
∴S四边形ACBP=S△APB+S△ABC=![]() =
=![]() +1;
+1;
④如图6,四边形ABPC是“准等边四边形”,过P作PF⊥AC于F,连接AP,
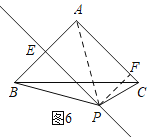
∵AB=AC=PB=![]() ,
,
∴PE=![]() ,
,
S四边形ABPC=S△APB+S△APC=![]() .
.

 同步练习强化拓展系列答案
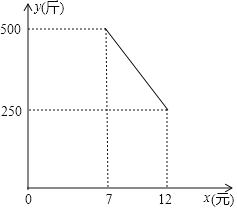
同步练习强化拓展系列答案【题目】商场里某产品每月销售量y(只)与销售单价x(元)满足一次函数关系,经调查部分数据如表:(已知每只进价为10元,每只利润=销售单价-进价)
销售单价x(元) | 21 | 23 | 25 | … |
月销售额y(只) | 29 | 27 | 25 | … |
(1)求出y与x之间的函数表达式;
(2)这产品每月的总利润为w元,求w关于x的函数表达式,并指出销售单价为多少元时利润最大,最大利润是多少元?
(3)由于该产品市场需求量较大,进价在原有基础上提高了a元(a<10),但每月销售量与销售价仍满足上述一次函数关系,此时,随着销售量的增大,所得的最大利润比(2)中的最大利润减少了144元,求a的值.