题目内容
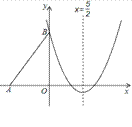
【题目】如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线![]() 经过点B,且顶点在直线
经过点B,且顶点在直线![]() 上.
上.
(1)求抛物线对应的函数关系式;
(2)若把△ABO沿x轴向右平移得到△DCE,点A、B、O的对应点分别是D、C、E,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
【答案】(1)![]() ;(2)点C和点D都在所求抛物线上.
;(2)点C和点D都在所求抛物线上.
【解析】试题分析:(1)根据抛物线![]() 经过点B(0,4),且顶点在直线
经过点B(0,4),且顶点在直线![]() 上,可求得b、c的值,即可得抛物线对应的函数关系式;(2)根据勾股定理求得AB的长,再根据四边形ABCD是菱形求得C、D两点的坐标,分别代入解析式即可判定点C和点D是否在该抛物线上.
上,可求得b、c的值,即可得抛物线对应的函数关系式;(2)根据勾股定理求得AB的长,再根据四边形ABCD是菱形求得C、D两点的坐标,分别代入解析式即可判定点C和点D是否在该抛物线上.
试题解析:
(1)∵抛物线![]() 经过B(0,4),∴c=4
经过B(0,4),∴c=4
∵顶点在直线![]() 上,∴
上,∴![]() ,
,![]()
∴所求的函数关系式为:![]()
(2)在Rt△ABO中,OA=3,OB=4,∴AB=![]() =5
=5
∵四边形ABCD是菱形,∴BC=CD=DA=AB=5,
∴C、D两点的坐标分别是(5,4)、(2,0),
当x=5时,![]()
当x=2时,![]()
∴点C和点D都在所求抛物线上.

练习册系列答案
相关题目


