题目内容
【题目】如图，正方形ABCD的对角线相交于点O，BC=6，延长BC至点E，使得CE=8，点F是DE的中点，连接CF、OF．
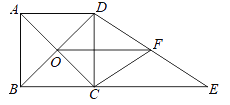
（1）求OF的长．
（2）求CF的长．
【答案】（1）7；（2）5．
【解析】试题分析：（1）由正方形的性质可知O为BD的中点，故此OF是△DBE的中位线，然后依据三角形中位线的性质解答即可；
（2）在Rt△DCE中，利用勾股定理求出DE，再利用直角三角形斜边上中线等于斜边的一半求解即可.
试题解析：（1）∵四边形ABCD是正方形，
∴BC=CD=6，∠BCD=∠ECD=90°，OB=OD，
∵CE=8，
∴BE=14，
∵OB=OD，DF=FE，
∴OF=
BE=7；
（2）在Rt△DCE中，DE=
=10，
∵DF=FE，
∴CF=
DE=5.
练习册系列答案
同步练习强化拓展系列答案
相关题目
