Question

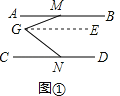
【题目】如图，已知AB∥CD，点M，N分别是AB，CD上两点，点G在AB，CD之间．

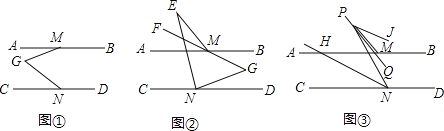
（1）求证：∠AMG+∠CNG＝∠MGN；

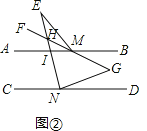
（2）如图②，点E是AB上方一点，MF平分∠AME，若点G恰好在MF的反向延长线上，且NE平分∠CNG，2∠E+∠G＝90°，求∠AME的度数；

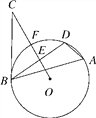
（3）如图③，若点P是（2）中的EM上一动点，PQ平分∠MPQ．NH平分∠PNC，交AB于点H，PJ∥NH，直接写出∠JPQ的度数．

Answer 1

【答案】（1）见解析；（2）∠AME＝60°；（3）∠JPQ＝30°．

【解析】

（1）过点G作GE∥AB，得出AB∥CD∥GE，再由平行线的性质即可得出结论；

（2）设FG与NE交点为H点，AB与NE的交点I，由三角形内角和定理可知∠G+∠HNG+∠NHG＝180°，再利用角平分线定理得出即90°+∠AME＝180°，继而得出结论；

（3）根据PQ平分∠MPN，NH平分∠PNC，可得出∠JPQ＝∠JPN﹣∠MPN，由此得出结论．

解：（1）证明：如图①，过点G作GE∥AB，

∵AB∥CD，

∴AB∥CD∥GE，

∴∠AMG＝∠MGE，∠CNG＝∠NGE，

∴∠AMG+∠CNG＝∠MGN；

（2）如图②，设FG与NE交点为H点，AB与NE的交点I，

在△HNG中，

∵∠G+∠HNG+∠NHG＝180°

∴∠HNG＝∠AIE＝∠IHM+∠IMH＝（∠E+∠EMF）+∠IMH＝∠E+（∠EMF+∠IMH ）＝∠E+∠AME

∠NHG＝∠IHM＝∠E+∠EMF＝∠E+∠AME

∴∠G+∠HNG+∠NHG＝∠G+（∠E+∠AME）+（∠E+∠AME）＝180° （∠G+2∠E）+∠AME＝180°，即90°+∠AME＝180°，

∴∠AME＝60°；

（3）∵PQ平分∠MPN，NH平分∠PNC，

∴∠JPQ＝∠JPN﹣∠MPN

＝（∠ENC﹣∠MPN）

＝（∠AOE﹣∠MPN）

＝∠AME

＝30°．