Question

【题目】如图，已知O为直线AD上一点，∠AOC与∠AOB互补，OM、ON分别是∠AOC、∠AOB的平分线，∠MON＝56°.

⑴ ∠COD与∠AOB相等吗？请说明理由；

⑵ 求∠BOC的度数；

⑶ 求∠AOB与∠AOC的度数.

Answer 1

【答案】（1）∠COD＝∠AOB.理由见解析；（2）∠BOC＝112°；（3）∠AOC＝146°.

【解析】试题分析：(1)根据题意可得∠AOC+∠AOB＝180°, ∠AOC+∠COD＝180°,可以根据同角的补角相等得到∠COD＝∠AOB;

（2）根据OM、ON分别是∠AOC、∠AOB的平分线可得∠AOM＝∠COM，∠AON＝∠BON，再利用教的和差可得∠BOC＝2 ∠MON；

(3)由（1）得∠COD＝∠AOB, 再根据∠AOB+∠BOC+∠COD＝180°可求出∠AOB的度数，然后根据平角的定义即可得到∠AOC.

解：⑴∠COD＝∠AOB.理由如下：

如图 ∵点O在直线AD上

∴∠AOC+∠COD＝180°

又∵∠AOC与∠AOB互补

∴∠AOC+∠AOB＝180°

∴∠COD＝∠AOB

⑵∵ OM、ON分别是∠AOC、∠AOB的平分线

∴∠AOM＝∠COM，∠AON＝∠BON

∴∠BOC＝∠BOM+∠COM＝∠BOM+∠AOM＝（∠MON－∠BON）+（∠MON+∠AON）＝2 ∠MON＝112°

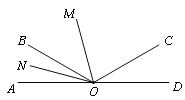
⑶由⑴得：∠COD＝∠AOB

∵ ∠AOB+∠BOC+∠COD＝180°

∴ ∠AOB＝（180°－∠BOC）＝（180°－112°）=34°

∴ ∠AOC＝180°－∠AOB＝180°－34°＝146°.