题目内容
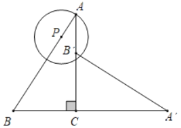
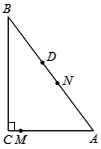
【题目】△ABC中,∠C=90°,点D在边AB上,AD=AC=7,BD=![]() BC.动点M从点C出发,以每秒1个单位的速度沿CA向点A运动,同时,动点N从点D出发,以每秒2个单位的速度沿DA向点A运动.当一个点到达点A时,点M、N两点同时停止运动.设M、N运动的时间为t秒.
BC.动点M从点C出发,以每秒1个单位的速度沿CA向点A运动,同时,动点N从点D出发,以每秒2个单位的速度沿DA向点A运动.当一个点到达点A时,点M、N两点同时停止运动.设M、N运动的时间为t秒.
(1)求cosA的值.
(2)当以MN为直径的圆与△ABC一边相切时,求t的值.
【答案】(1)![]() ;(2)t=1或t=2.
;(2)t=1或t=2.
【解析】
试题(1)设BC=4m,AC=x,用m表示出AC和AB,根据三角函数定义即可求解.
(2)分⊙O与AB相切,⊙O与AC相切和⊙O与BC相切三种情况讨论即可.
(1)设BC=4m,AC=x,则BD=2m,AD=x,
∵![]() ,∴ 16
,∴ 16![]() +
+![]() =
=![]() . 解之得 x=3m.
. 解之得 x=3m.
从而AB=5m.
因此cosA=![]() .
.
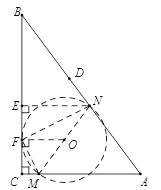
(2)CM=t,AM=7-t,DN=2t,AN=7-2t,其中0≤t≤3.5,
记以MN为直径的圆为⊙O,当⊙O与AB相切时,则MN⊥AB,
因此![]()
![]() ,t=2,符合题意;
,t=2,符合题意;
当⊙O与AC相切时,则MN⊥AC,因此![]() ,t=-14,舍去;
,t=-14,舍去;
当⊙O与BC相切时,如图,作NE⊥BC,垂足为E.取EC的中点F,连结OF,则OF⊥BC,即点F为⊙O与BC相切的切点.连结MF,NF,则FM⊥FN,因此△FCM∽△NEF.
因此CM·EN=![]() .
.
而CM=t,EN=![]() ,EF=FC=
,EF=FC=![]() EC=
EC=![]() ,
,
因此![]() ,整理得
,整理得![]() ,解之得 t=1,t=-14(舍去) .
,解之得 t=1,t=-14(舍去) .
综上所得,当以MN为直径的圆与△ABC一边相切时,t=1或t=2.

练习册系列答案
 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目