题目内容
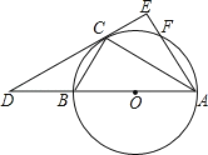
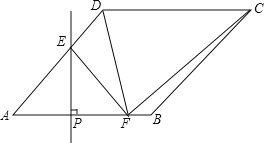
【题目】如图,在菱形![]() 中,
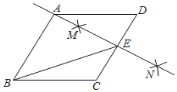
中,![]() ,按以下步骤作图:①分别以点
,按以下步骤作图:①分别以点![]() 和点
和点![]() 为圆心,为圆心,大于号
为圆心,为圆心,大于号![]() 的长为半径面狐,两弧交于点
的长为半径面狐,两弧交于点![]() ,
,![]() :②做直线
:②做直线![]() ,且
,且![]() 恰好经过点
恰好经过点![]() ,与
,与![]() 交于点
交于点![]() ,连接
,连接![]() ,则
,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
由作法得AE垂直平分CD,则∠AED=90°,CE=DE,于是可判断∠DAE=30°,∠D=60°,作EH⊥BC于H,从而得到∠ECH=60°,利用三角函数可求出EH、CH的值,再利用勾股定理即可求出BE的长.
解:如图所示,作EH⊥BC于H,
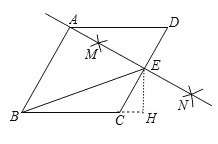
由作法得AE垂直平分CD,
∴∠AED=90°,CE=DE=2,
∵四边形ABCD为菱形,
∴AD=2DE,
∴∠DAE=30°,
∴∠D=60°,
∵AD//BC,
∴∠ECH=∠D=60°,
在Rt△ECH中,
EH=CE·sin60°=![]() ,
,
CH=CE·cos60°=![]() ,
,
∴BH=4+1=5,
在Rt△BEH中,由勾股定理得,
![]() .
.
故选B.

练习册系列答案
相关题目
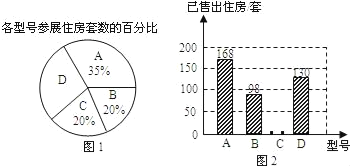
【题目】每年5月20日是中国学生营养日,按时吃早餐是一种健廉的饮食习惯,为了解本校九年级学生饮食习惯,某兴趣小组在九年级随机抽查了一部分学生每天吃早餐的情况,并将统计结果绘制成如下不完
整的统计图表:
组别 | 调查结果 | 所占百分比 |
A | 不吃早餐 | 25% |
B | 偶尔吃早餐 | 12.5% |
C | 经常吃早餐 | |
D | 每天吃早餐 | 50% |

请根据以上统计图表,解答下列问题:
(1)本次接受调查的总人数为多少人.
(2)请补全条形统计图.
(3)该校九年级共有学生1200人,请估计该校九年级学生每天吃早餐的人数:
(4)请根据此次调查的结果提一条建议.