题目内容
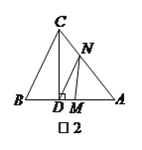
【题目】已知:如图,在矩形ABCD中,AB=8,BC=4.在AD上取一点E,AE=1,点F是AB边上的一个动点,以EF为一边作菱形EFMN,使点N落在CD边上,点M落在矩形ABCD内或其边上.若AF=x,△BFM的面积为S.
(1)当四边形EFMN是正方形时,求x的值;

(2)当四边形EFMN是菱形时,求S与x的函数关系式;

(3)当x= 时,△BFM的面积S最大;当x= 时,△BFM的面积S最小;
(4)在△BFM的面积S由最大变为最小的过程中,请直接写出点M运动的路线长: 。


【答案】(1)x=3;(2)S=![]() ;(3)
;(3)![]() ;(4)
;(4) ![]()
【解析】
(1)利用AAS证明△DEN≌△AFE即可解决问题;
(2)如图,过点M作MH⊥AB于H,连接NF,证明△DEN≌△HMF,可得MH=DE=3,由此即可解决问题;
(3)①如备用图①中,当点N与点D重合时,x的值最小,△FBM的面积最大,在Rt△AEF中,x=![]() ,推出S的最大值=12-3
,推出S的最大值=12-3![]() ;②如备用图②,当点M在BC上时,x的值最大,△FBM的面积最小;
;②如备用图②,当点M在BC上时,x的值最大,△FBM的面积最小;
(4)如备用图③中,在△BFM的面积S由最大变为最小的过程中,点M的运动轨迹是平行AB的线段,点M运动的路线长=BF的长=8-2![]() .
.
(1)在正方形EFMN中,∠FEN=90°,EF=EN,
∴ ∠DEN+∠AEF=90°,
在矩形ABCD中,∠A=∠D=90°,
∴ ∠AEF+∠AFE=90°,
∴ ∠DEN=∠AFE,
在△DEN与△AFE中,
 ,
,
∴△DEN≌△AFE(AAS),
∴AF=DE=4-1=3,
∴x的值为3;
(2)过点M作MH⊥AB于H,连接NF,
在矩形ABCD中,∵AB∥CD,
∴∠DNF=∠NFB,
∵四边形EFMN是菱形,
∴NE‖MF ,NE=MF,
∴∠ENF=∠MFN,
∴∠DNE=∠MFB ,
在△DEN与△HMF中,
 ,
,
∴△DEN≌△HMF(AAS),
∴MH=DE=3,BF=8-x,
![]() ;
;

(3)①如备用图①中,当点N与点D重合时,x的值最小,△FBM的面积最大,
在Rt△AEF中,x=![]() ,
,
∴S的最大值=12-3![]() ;
;
②如备用图②,当点M在BC上时,x的值最大,△FBM的面积最小,
此时易得CN=AF=x,
∵EN=EF,
∴12+x2=32+(8-x)2,
∴x=![]() ,
,
∴S的最小值为![]() ,
,
故答案为:2![]() ,
,![]() ;
;
(4)如备用图③中,在△BFM的面积S由最大变为最小的过程中,点M的运动轨迹是平行AB的线段,点M运动的路线长=BF的长=8-2![]() ,
,
故答案为:![]() .
.