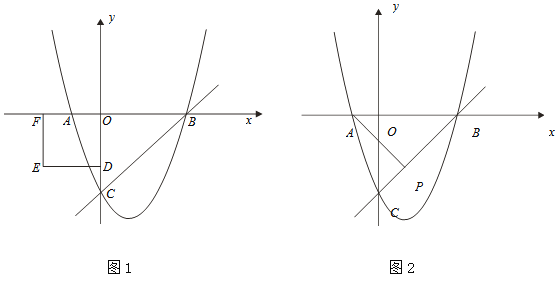
��Ŀ����
����Ŀ����֪������![]() ��y�ύ��C�㣬��x�ύ��A��B���㣬��A�������ǣ�-1,0����O������ԭ�㣬��
��y�ύ��C�㣬��x�ύ��A��B���㣬��A�������ǣ�-1,0����O������ԭ�㣬��![]() ��
��
��1���������ߵĺ�������ʽ��
��2��ֱ��д��ֱ��BC�ĺ�������ʽ��
��3����ͼ1��DΪy��ĸ������ϵ�һ�㣬��OD=2����ODΪ����������ODEF.��������ODEF��ÿ��1����λ���ٶ���x����������ƶ������˶������У���������ODEF���OBC�ص����ֵ����Ϊs���˶���ʱ��Ϊt�루0��t��2��.��s��t֮��ĺ�����ϵʽ�� �����˶������У�s�Ƿ�������ֵ��������ڣ�ֱ��д��������ֵ����������ڣ���˵�����ɣ�
��4����ͼ2����P��1��k����ֱ��BC�ϣ���M��x���ϣ���N���������ϣ��Ƿ������A��M��N��PΪ�����ƽ���ı��Σ������ڣ���ֱ��д��M�����ꣻ�������ڣ���˵������.
���𰸡���1��y=x2��2x��3����2��y=x��3����3���ٵ�0��t��1ʱ��S1=2t����1��t��2ʱ��S2=��![]() ���ڵ�t=2��ʱ��S�����ֵ�����ֵΪ
���ڵ�t=2��ʱ��S�����ֵ�����ֵΪ![]() ����4��M 1����
����4��M 1����![]() ��
��![]() ����M2��
����M2��![]() ��
��![]() ����M3��
����M3��![]() ��
��![]() ����M4��
����M4��![]() ��
��![]() ��
��
��������������(1)����OC��OA��������ϵȷ����C�����꣬Ȼ�����ô���ϵ��������������ߵĽ���ʽ; (2)��(1)�������߽���ʽ�ɵõ�B�����꣬��ϵ�C�����꣬���ô���ϵ������⼴��; (3)������Ҫ��ȷ������ODEF�͡�OBC�غϲ��ֵ���״������D�ڡ�OBC�ڲ�ʱ�����ߵ��غϲ����Ǿ��Σ�����D�ڡ�OBC�ⲿʱ�����ߵ��غϲ���������Σ���������������ε������ȥ�� �����(G��H�ֱ�Ϊ �� ���߶�BC�Ľ���)�����ж�t��ȡֵ��Χʱ��Ҫע��һ�����ؼ��㡱����Dλ���߶�BC��ʱ; �ڸ��ݢٵĺ������ʼ��ɵõ��𰸣� (4)��������A��M��N��PΪ�����ƽ���ı��Σ�Ӧ��AM PN��AN PM�������.����AM��x���ϣ����ƽ���ı��ε��ص��֪�����������������N��x��ľ��붼���ڵ�P��x��ľ��룬��������ص��ȷ����M��N�����꣮
�����������1���� A��-1,0��, ![]() ,C��0,-3��
,C��0,-3��
�������߾���A��-1,0��,C��0,-3��
��![]() ����
����![]() ��
��
��y=x2��2x��3
(2)��(1)�������߽���ʽ��֪����B(3��0).
��ֱ��BC�Ľ���ʽΪy=kx+b.
��B(3��0)��C(0��-3)�����![]() �����
�����![]() ��
��
��ֱ��BC�ĺ�������ʽΪy=x-3��
��3����������ODEF�Ķ���D�˶���ֱ��BC��ʱ����D�������Ϊ��m��-2����
��������ã� -2=m-3����m=1
�ٵ�0��t��1ʱ��S1=2t
��1��t��2ʱ
S2=![]() =2t��
=2t��![]()
=��![]() ��
��
�ڵ�t =2��ʱ��S�����ֵ�����ֵΪ![]()
��4����(2)֪����P(1��-2)��������ڷ��������ĵ�M.
�ٵ�AM��PN��AM=PNʱ����N��P����������ͬ��
����N��������Ϊ-2�����������ߵĽ���ʽ�е�x-2x-3=-2��
��� x=1��![]() ��
��
��AM=NP=![]() ��
��
��M 1����![]() ��0�� M2
��0�� M2![]() ��0��,
��0��,
�ڵ�AN��PM,AN=PMʱ��ƽ���ı��εĶԽ���PN��AM����ƽ��.
��M(m��0)����N(m-2��2).
����N��������������ߵĽ���ʽ�У���(m-2)-2(m-2)-3=2��
��� m=3��![]() ��
��
��M3��3-![]() ��0�� M4��3+
��0�� M4��3+![]() ��0 ����
��0 ����
���ϣ����ڷ���������M�㣬������Ϊ��
M 1����![]() ��0�� M2��
��0�� M2��![]() ��0��
��0��
M3��3-![]() ��0�� M4��3+
��0�� M4��3+![]() ��0 ��
��0 ��