ЬтФПФкШн
ЁОЬтФПЁПЪ§жсЪЧвЛИіЗЧГЃживЊЕФЪ§бЇЙЄОпЃЌЫќЪЙЪ§КЭЪ§жсЩЯЕФЕуНЈСЂЦ№ЖдгІЙиЯЕЃЌНвЪОСЫЪ§гыЕужЎМфЕФФкдкСЊЯЕЃЌЫќЪЧЁАЪ§аЮНсКЯЁБЕФЛљДЁЁЃаЁАздкВнИхжНЩЯЛСЫвЛЬѕЪ§жсНјааВйзїЬНОПЃК
ВйзївЛЃК
ЃЈ1ЃЉелЕўжНУцЃЌШєЪЙ1БэЪОЕФЕугыЉ1БэЪОЕФЕужиКЯЃЌдђЉ2БэЪОЕФЕугы_______БэЪОЕФЕужиКЯЃЛ
ВйзїЖўЃК
ЃЈ2ЃЉелЕўжНУцЃЌШєЪЙ1БэЪОЕФЕугыЉ3БэЪОЕФЕужиКЯЃЌЛиД№вдЯТЮЪЬтЃК
Ђй3БэЪОЕФЕугы_______БэЪОЕФЕужиКЯЃЛ
ЂкШєЪ§жсЩЯAЁЂBСНЕужЎМфОрРыЮЊ7ЃЈAдкBЕФзѓВрЃЉЃЌЧвAЁЂBСНЕуОелЕўКѓжиКЯЃЌдђAЁЂBСНЕуБэЪОЕФЪ§ЗжБ№ЪЧ______________ЃЛ
ВйзїШ§ЃК
ЃЈ3ЃЉдкЪ§жсЩЯМєЯТ9ИіЕЅЮЛГЄЖШЃЈДгЉ1ЕН8ЃЉЕФвЛЬѕЯпЖЮЃЌВЂАбетЬѕЯпЖЮбиФГЕуелЕўЃЌШЛКѓдкжиЕўВПЗжФГДІМєвЛЕЖЕУЕНШ§ЬѕЯпЖЮЃЈР§ШчЯТЭМЃЉ. ШєетШ§ЬѕЯпЖЮЕФГЄЖШжЎБШЮЊ1ЃК1ЃК2ЃЌдђелКлДІЖдгІЕФЕуЫљБэЪОЕФЪ§ПЩФмЪЧ_____________________.

ЁОД№АИЁПЃЈ1ЃЉ2 ЃЈ2ЃЉЂй-5ЃЛЂк-![]() ,
,![]() ЃЈ3ЃЉ
ЃЈ3ЃЉ![]() Лђ
Лђ![]() Лђ
Лђ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнЖдГЦадевЕНелКлЕФЕуЮЊдЕуOЃЌПЩвдЕУГі-2гы2жиКЯЃЛ
ЃЈ2ЃЉИљОнЖдГЦадевЕНелКлЕФЕуЮЊ-1ЃЌ
ЂйЩш3БэЪОЕФЕугыЪ§aБэЪОЕФЕужиКЯЃЌИљОнЖдГЦадСаЪНЧѓГіaЕФжЕЃЛ
ЂквђЮЊAB=7ЃЌЫљвдAЕНелКлЕФЕуОрРыЮЊ3.5ЃЌвђЮЊелКлЖдгІЕФЕуЮЊ-1ЃЌгЩДЫЕУГіAЁЂBСНЕуБэЪОЕФЪ§ЃЛ
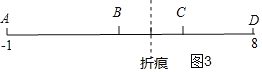
ЃЈ3ЃЉЗжШ§жжЧщПіНјааЬжТлЃКЩшелКлДІЖдгІЕФЕуЫљБэЪОЕФЪ§ЪЧxЃЌШчЭМ1ЃЌЕБABЃКBCЃКCD=1ЃК1ЃК2ЪБЃЌЩшAB=aЃЌBC=aЃЌCD=2aЃЌЕУa+a+2a=9ЃЌa=![]() ЃЌЕУГіABЁЂBCЁЂCDЕФжЕЃЌМЦЫуЕУxЕФжЕЃЌЭЌРэПЩЕУГіШчЭМ2ЁЂ3ЖдгІЕФxЕФжЕЃЎ
ЃЌЕУГіABЁЂBCЁЂCDЕФжЕЃЌМЦЫуЕУxЕФжЕЃЌЭЌРэПЩЕУГіШчЭМ2ЁЂ3ЖдгІЕФxЕФжЕЃЎ
ЪдЬтНтЮіЃКВйзївЛЃЌ
ЃЈ1ЃЉЁпБэЪОЕФЕу1гы-1БэЪОЕФЕужиКЯЃЌ
ЁрелКлЮЊдЕуOЃЌ
дђ-2БэЪОЕФЕугы2БэЪОЕФЕужиКЯ.
ВйзїЖўЃК
ЃЈ2ЃЉЁпелЕўжНУцЃЌШєЪЙ1БэЪОЕФЕугы-3БэЪОЕФЕужиКЯЃЌ
дђелКлБэЪОЕФЕуЮЊ-1ЃЌ
ЂйЩш3БэЪОЕФЕугыЪ§aБэЪОЕФЕужиКЯЃЌ
дђ3-ЃЈ-1ЃЉ=-1-aЃЌ
a=-5ЃЛ
ЂкЁпЪ§жсЩЯAЁЂBСНЕужЎМфОрРыЮЊ7ЃЌ
ЁрЪ§жсЩЯAЁЂBСНЕуЕНелКл-1ЕФОрРыЮЊ3.5ЃЌ
ЁпAдкBЕФзѓВрЃЌ
дђAЁЂBСНЕуБэЪОЕФЪ§ЗжБ№ЪЧ-4.5КЭ2.5ЃЛ
ВйзїШ§ЃК
ЃЈ3ЃЉЩшелКлДІЖдгІЕФЕуЫљБэЪОЕФЪ§ЪЧxЃЌ
ШчЭМ1ЃЌ
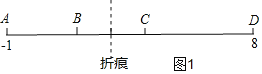
ЕБABЃКBCЃКCD=1ЃК1ЃК2ЪБЃЌ
ЩшAB=aЃЌBC=aЃЌCD=2aЃЌ
a+a+2a=9ЃЌ
a=![]() ЃЌ
ЃЌ
ЁрAB=![]() ЃЌBC=
ЃЌBC=![]() ЃЌCD=
ЃЌCD=![]() ЃЌ
ЃЌ
x=-1+![]() +
+![]() =
=![]() ЃЌ
ЃЌ
ШчЭМ2ЃЌ
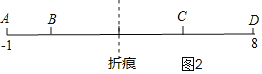
ЕБABЃКBCЃКCD=1ЃК2ЃК1ЪБЃЌ
ЩшAB=aЃЌBC=2aЃЌCD=aЃЌ
a+a+2a=9ЃЌ
a=![]() ЃЌ
ЃЌ
ЁрAB=![]() ЃЌBC=
ЃЌBC=![]() ЃЌCD=
ЃЌCD=![]() ЃЌ
ЃЌ
x=-1+![]() +
+![]() =
=![]() ЃЌ
ЃЌ
ШчЭМ3ЃЌ
ЕБABЃКBCЃКCD=2ЃК1ЃК1ЪБЃЌ
ЩшAB=2aЃЌBC=aЃЌCD=aЃЌ
a+a+2a=9ЃЌ
a=![]() ЃЌ
ЃЌ
ЁрAB=![]() ЃЌBC=CD=
ЃЌBC=CD=![]() ЃЌ
ЃЌ
x=-1+![]() +
+![]() =
=![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃКдђелКлДІЖдгІЕФЕуЫљБэЪОЕФЪ§ПЩФмЪЧ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЎ
ЃЎ