Question

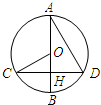如图，AB为⊙O的直径，弦CD⊥AB于点H，连接OC，AD，若BH：CO=1：2，AD=4

3

，则⊙O的周长等于

 

．

Answer 1

分析：已知BH：CO=1：2，即BH=OH=

1

2

OC；在Rt△OCH中，易求得∠COH=60°；
由于弧BC=弧BD（垂径定理），利用圆心角和圆周角的关系可求得∠DAB=30°；
在Rt△ADH中，可求得DH的长；也就求出了CH的长，在Rt△COH中，根据∠COH的正弦值和CH的长，即可求出OC的半径，进而可求出⊙O的周长．

解答：解：∵半径OB⊥CD，
∴

BC

=

BD

，CH=DH；（垂径定理）
∵BH：CO=1：2，
∴BH=OH=

1

2

OC；
在Rt△OCH中，OH=

1

2

OC，
∴∠COH=60°；
∵

BC

=

BD

，
∴∠DAH=

1

2

∠COH=30°；（圆周角定理）
在Rt△AHD中，∠DAH=30°，AD=4

3

，则DH=CH=2

3

；
在Rt△OCH中，∠COH=60°，CH=2

3

，则OC=4．
∴⊙O的周长为8π．

点评：本题考查的是圆周角定理、垂径定理、锐角三角函数等知识的综合应用．解答这类题一些学生不会综合运用所学知识解答问题，不知从何处入手造成错解．