题目内容
已知抛物线 与y轴交于C点,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且
与y轴交于C点,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且 .
.
(1)求抛物线的函数表达式;
(2)直接写出直线BC的函数表达式;
(3)如图1,D为y轴的负半轴上的一点,且OD=2,以OD为边作正方形ODEF.将正方形ODEF
以每秒1个单位的速度沿x轴的正方向移动,在运动过程中,设正方形ODEF与△OBC重叠部分的面积为s,运动的时间为t秒(0<t≤2).
求:①s与t之间的函数关系式; ②在运动过程中,s是否存在最大值?如果存在,直接写出这个最大值;如果不存在,请说明理由.
(4)如图2,点P(1,k)在直线BC上,点M在x轴上,点N在抛物线上,是否存在以A、M、
N、P为顶点的平行四边形?若存在,请直接写出M点坐标;若不存在,请说明理由.
 与y轴交于C点,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且
与y轴交于C点,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且 .
.(1)求抛物线的函数表达式;
(2)直接写出直线BC的函数表达式;
(3)如图1,D为y轴的负半轴上的一点,且OD=2,以OD为边作正方形ODEF.将正方形ODEF
以每秒1个单位的速度沿x轴的正方向移动,在运动过程中,设正方形ODEF与△OBC重叠部分的面积为s,运动的时间为t秒(0<t≤2).
求:①s与t之间的函数关系式; ②在运动过程中,s是否存在最大值?如果存在,直接写出这个最大值;如果不存在,请说明理由.
(4)如图2,点P(1,k)在直线BC上,点M在x轴上,点N在抛物线上,是否存在以A、M、
N、P为顶点的平行四边形?若存在,请直接写出M点坐标;若不存在,请说明理由.

(1)y=x2-2x-3(2)直线BC的函数表达式为y=x-3(3)①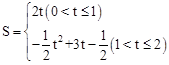 ②当t =2秒时,S有最大值,最大值为
②当t =2秒时,S有最大值,最大值为 (4)存在。M 1(-
(4)存在。M 1(-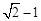 ,0)M2(
,0)M2(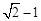 ,0),M3(
,0),M3(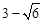 ,0),M4(
,0),M4(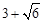 ,0)
,0)
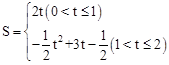 ②当t =2秒时,S有最大值,最大值为
②当t =2秒时,S有最大值,最大值为 (4)存在。M 1(-
(4)存在。M 1(-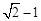 ,0)M2(
,0)M2(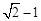 ,0),M3(
,0),M3(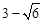 ,0),M4(
,0),M4(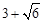 ,0)
,0)解:(1)∵ A(-1,0),  ,∴C(0,-3)。
,∴C(0,-3)。
∵抛物线经过A(-1,0),C(0,,3),
∴ ,解得
,解得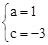 。
。
∴抛物线的函数表达式y=x2-2x-3。
(2)直线BC的函数表达式为y=x-3。
(3)当正方形ODEF的顶点D运动到直线BC上时,设D点的坐标为(m,-2),
根据题意得:-2=m-3,∴m=1。
①当0<t≤1时,S1=2t;
当1<t≤2时,如图,
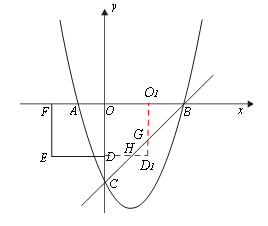
O1(t,0),D1(t,-2),
G(t,t-3),H(1,-2),
∴GD1=t-1,HD1= t-1。
∴S=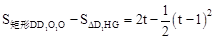
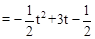 。
。
∴s与t之间的函数关系式为
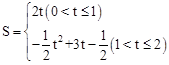
②在运动过程中,s是存在最大值:当t =2秒时,S有最大值,最大值为 。
。
(4)存在。M 1(-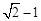 ,0)M2(
,0)M2(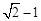 ,0),M3(
,0),M3(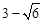 ,0),M4(
,0),M4(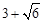 ,0)。
,0)。
(1)求出点C的坐标,即可根据A,C的坐标用待定系数法求出抛物线的函数表达式。
(2)求出点B的坐标(3,0),即可由待定系数法求出直线BC的函数表达式。
(3)①分0<t≤1和1<t≤2讨论即可。
②由于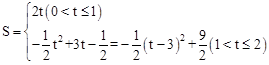 在0<t≤2上随t的增大而增大,从而在运动过程中,s是存在最大值:当t =2秒时,S有最大值,最大值为
在0<t≤2上随t的增大而增大,从而在运动过程中,s是存在最大值:当t =2秒时,S有最大值,最大值为 。
。
(4)由点P(1,k)在直线BC上,可得k=-2。∴P(1,-2)。
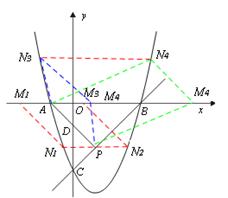
则过点P且平行于x轴的直线N1N2和在x轴上方与x轴的距离为2的直线N3N4,与y=x2-2x-3的交点N1、N2、 N3、N4的坐标分别为N1(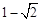 ,-2),N2(
,-2),N2(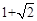 ,-2), N3(
,-2), N3(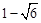 , 2),N4(
, 2),N4(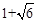 , 2)。
, 2)。
则M1的横坐标为-PN1加点A的横坐标:-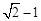 ;
;
M2的横坐标为PN2加点A的横坐标: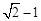 ;
;
M3的横坐标为N3的纵坐标加N3的横坐标: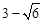 ;
;
M4的横坐标为N4的纵坐标加N4的的横坐标: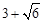 。
。
综上所述,M 1(-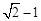 ,0)M2(
,0)M2(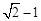 ,0),M3(
,0),M3(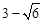 ,0),M4(
,0),M4(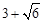 ,0)。
,0)。
 ,∴C(0,-3)。
,∴C(0,-3)。∵抛物线经过A(-1,0),C(0,,3),
∴
 ,解得
,解得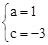 。
。∴抛物线的函数表达式y=x2-2x-3。
(2)直线BC的函数表达式为y=x-3。
(3)当正方形ODEF的顶点D运动到直线BC上时,设D点的坐标为(m,-2),
根据题意得:-2=m-3,∴m=1。
①当0<t≤1时,S1=2t;
当1<t≤2时,如图,

O1(t,0),D1(t,-2),
G(t,t-3),H(1,-2),
∴GD1=t-1,HD1= t-1。
∴S=
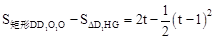
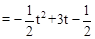 。
。∴s与t之间的函数关系式为
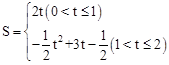
②在运动过程中,s是存在最大值:当t =2秒时,S有最大值,最大值为
 。
。(4)存在。M 1(-
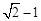 ,0)M2(
,0)M2(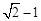 ,0),M3(
,0),M3(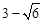 ,0),M4(
,0),M4(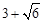 ,0)。
,0)。(1)求出点C的坐标,即可根据A,C的坐标用待定系数法求出抛物线的函数表达式。
(2)求出点B的坐标(3,0),即可由待定系数法求出直线BC的函数表达式。
(3)①分0<t≤1和1<t≤2讨论即可。
②由于
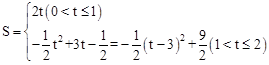 在0<t≤2上随t的增大而增大,从而在运动过程中,s是存在最大值:当t =2秒时,S有最大值,最大值为
在0<t≤2上随t的增大而增大,从而在运动过程中,s是存在最大值:当t =2秒时,S有最大值,最大值为 。
。(4)由点P(1,k)在直线BC上,可得k=-2。∴P(1,-2)。

则过点P且平行于x轴的直线N1N2和在x轴上方与x轴的距离为2的直线N3N4,与y=x2-2x-3的交点N1、N2、 N3、N4的坐标分别为N1(
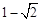 ,-2),N2(
,-2),N2(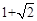 ,-2), N3(
,-2), N3(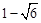 , 2),N4(
, 2),N4(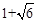 , 2)。
, 2)。则M1的横坐标为-PN1加点A的横坐标:-
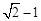 ;
;M2的横坐标为PN2加点A的横坐标:
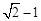 ;
;M3的横坐标为N3的纵坐标加N3的横坐标:
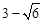 ;
;M4的横坐标为N4的纵坐标加N4的的横坐标:
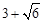 。
。综上所述,M 1(-
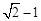 ,0)M2(
,0)M2(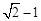 ,0),M3(
,0),M3(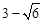 ,0),M4(
,0),M4(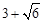 ,0)。
,0)。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 (台)
(台) (台)与月份x(月)之间存在如图所示的变化趋势:
(台)与月份x(月)之间存在如图所示的变化趋势:
 与x之间的函数关系式,根据如图所示的变化趋势,直接写出
与x之间的函数关系式,根据如图所示的变化趋势,直接写出 与x之间满足的一次函数关系式;
与x之间满足的一次函数关系式; (万元)与月份x满足函数关系式:
(万元)与月份x满足函数关系式:  ,(1≤x≤7,且x为整数);8至12月份的资金投入
,(1≤x≤7,且x为整数);8至12月份的资金投入 (万元)与月份x满足函数关系式:
(万元)与月份x满足函数关系式: (8≤x≤12,且x为整数)求去年哪个月政府对该片区的资金投入最大,并求出这个最大投入;
(8≤x≤12,且x为整数)求去年哪个月政府对该片区的资金投入最大,并求出这个最大投入;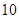 个档次,生产第一档次(即最低档次)的产品一天生产
个档次,生产第一档次(即最低档次)的产品一天生产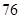 件,每件利润
件,每件利润 元.
元. 元时,此产品质量在第几档次?
元时,此产品质量在第几档次? 件.若生产第
件.若生产第 档的产品一天的总利润为
档的产品一天的总利润为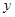 元(其中
元(其中 ≤
≤ 元,该工厂生产的是第几档次的产品?
元,该工厂生产的是第几档次的产品?
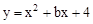 的图像向右平移3个单位,再向上平移2个单位,所得到的图象的解析式为
的图像向右平移3个单位,再向上平移2个单位,所得到的图象的解析式为 ,则b的值为【 】
,则b的值为【 】 ,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒
,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒 个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.